Benchmarking RK3588 NPU matrix multiplication performance EP2

Not long after my last benchmarking attempt. Rockchip releases a SDK update that fixes the crashing matrix multiplication API. Now I'm no longer restricted to using ONNX. Now I can directly do matrix multiplication from C! And now I can do an apple to apple comparison with OpenBLAS. That's benchmarking. Actually, I knew the SDK update days before writing this post. But I held on because I'm working on something more exiting - porting Large Language Models to run on RK3588 NPU. The result is.. well, you'll see. I also got an oppertunity to speak at Skymizer's interal tech forum because of my work. I'll share the side deck after I gave the talk.

RKNPU MatMul API

You can fine the MatMul API in the following link. The example proided is intimidating.. but it's actually not that hard to use once you get the hang of it. The API is very similar to older API designs like OpenGL.

First, you need to setup a descriptor of the kind of multiplication you want to do. This contains the shape of the input and output matrices. And the data type. Futhermore, it also contains the "foramt" of the input and output matrices. Currently only float16 and int8 are supported.

rknn_matmul_info info;
info.M             = M;
info.K             = K;
info.N             = N;
info.type          = RKNN_TENSOR_FLOAT16;
info.native_layout = 0;
info.perf_layout   = 0;

Shape of the matrix is pretty self explanatory if you ever used BLAS before. If not, consider the following Python code. 2 matrices are created. One is 64x128, the other is 128x256. According to the rule of matrix multiplication, the result should have a shape of 64x256. In code, this is represented by the M, K, N variables. Where M=64, K=128, N=256 in this case. Or have a look at the diagram below.

a = np.random.rand(64, 128)
b = np.random.rand(128, 256)
c = np.matmul(a, b)

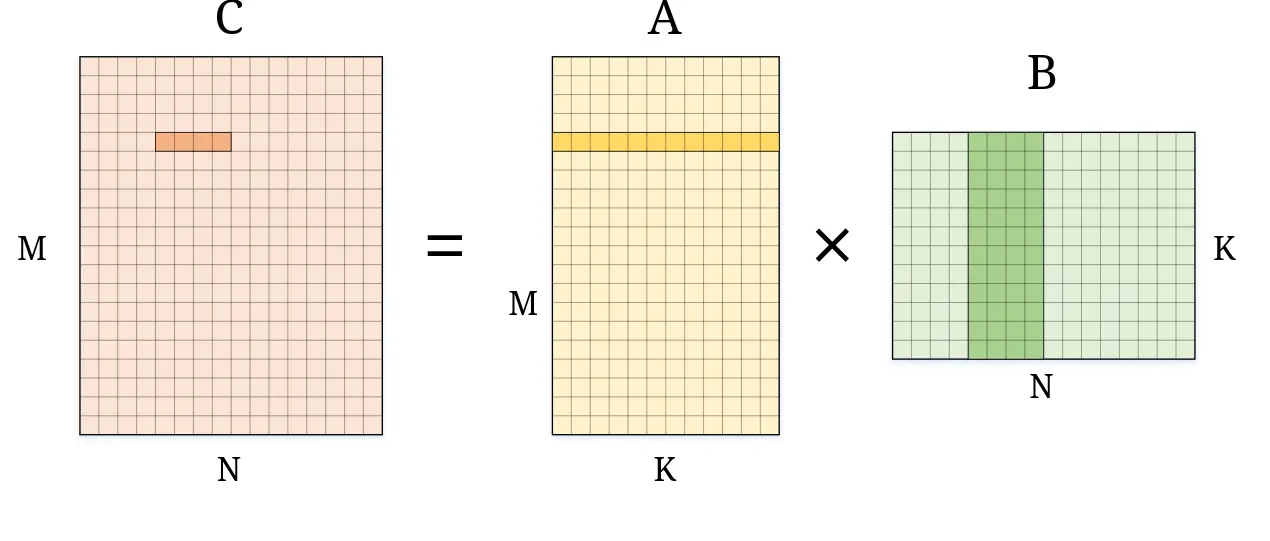
native_layout and perf_layout are the "format" of the input and output matrices. When set to 0, the matrix multiplication API works like you expected. The input and output matrices are stored in row-major order. However, the NPU does not perform well when multiplying matrices in row-major order. The runtime will reorder the matrices to an internal format sutible for the NPU before sending it for processing. This can be slow if you plan of multiplying multiple different matrices. Setting them to 1 will tell the runtime that you have already reordered the matrices and it can skip the reordering step.

We created the descriptor. Now we need to create the actual matrix multiplication object. This is done by calling rknn_matmul_create. The function takes the descriptor and gives you back a handle to the matrix multiplication object. And an IO descriptor. With these, we can call rknn_create_mem to allocate memory for the input and output matrices. Then rknn_matmul_set_io_mem to tell the matrix multiplication object where the input and output matrices are located.

rknn_matmul_io_attr io_attr;
rknn_matmul_ctx ctx;
rknn_matmul_create(&ctx, &info, &io_attr);

rknn_tensor_mem* A = rknn_create_mem(ctx, io_attr.A.size);
rknn_tensor_mem* B = rknn_create_mem(ctx, io_attr.B.size);
rknn_tensor_mem* C = rknn_create_mem(ctx, io_attr.C.size);

// For demo, we initialize the input matrices with 0
memcpy(A->virt_addr, a, io_attr.A.size);
memcpy(B->virt_addr, b, io_attr.B.size);

rknn_matmul_set_io_mem(ctx, A, &io_attr.A);
rknn_matmul_set_io_mem(ctx, B, &io_attr.B);
rknn_matmul_set_io_mem(ctx, C, &io_attr.C);

Finally, call rknn_matmul_run to perform the matrix multiplication. After the call, the result will be stored in the memory pointed by C->virt_addr.

rknn_matmul_run(ctx);

float* result = (float*)C->virt_addr;
// Do something with the result

Updating values for the input matrices

One thing to note is that the driver seems to create a copy of the input matrices. So if you want to update the values of the input matrices, you need to call rknn_matmul_set_io_mem again. Otherwise, the values will not be updated.

// Update the values of the input matrices
typedef __fp16 float16; // GCC 16-bit float extension
for (int i = 0; i < io_attr.A.size / sizeof(float); i++) {
    ((float16*)A->virt_addr)[i] = i;
}

// Remember to call rknn_matmul_set_io_mem again. Otherwise, the values will not be updated
rknn_matmul_set_io_mem(ctx, A, &io_attr.A);

Benchmarking

That's the gist of the API. Now let's benchmark it. The benchmarking code is pretty much the same as the last time. Except it's in C now and I have finer control over how it gets executed.

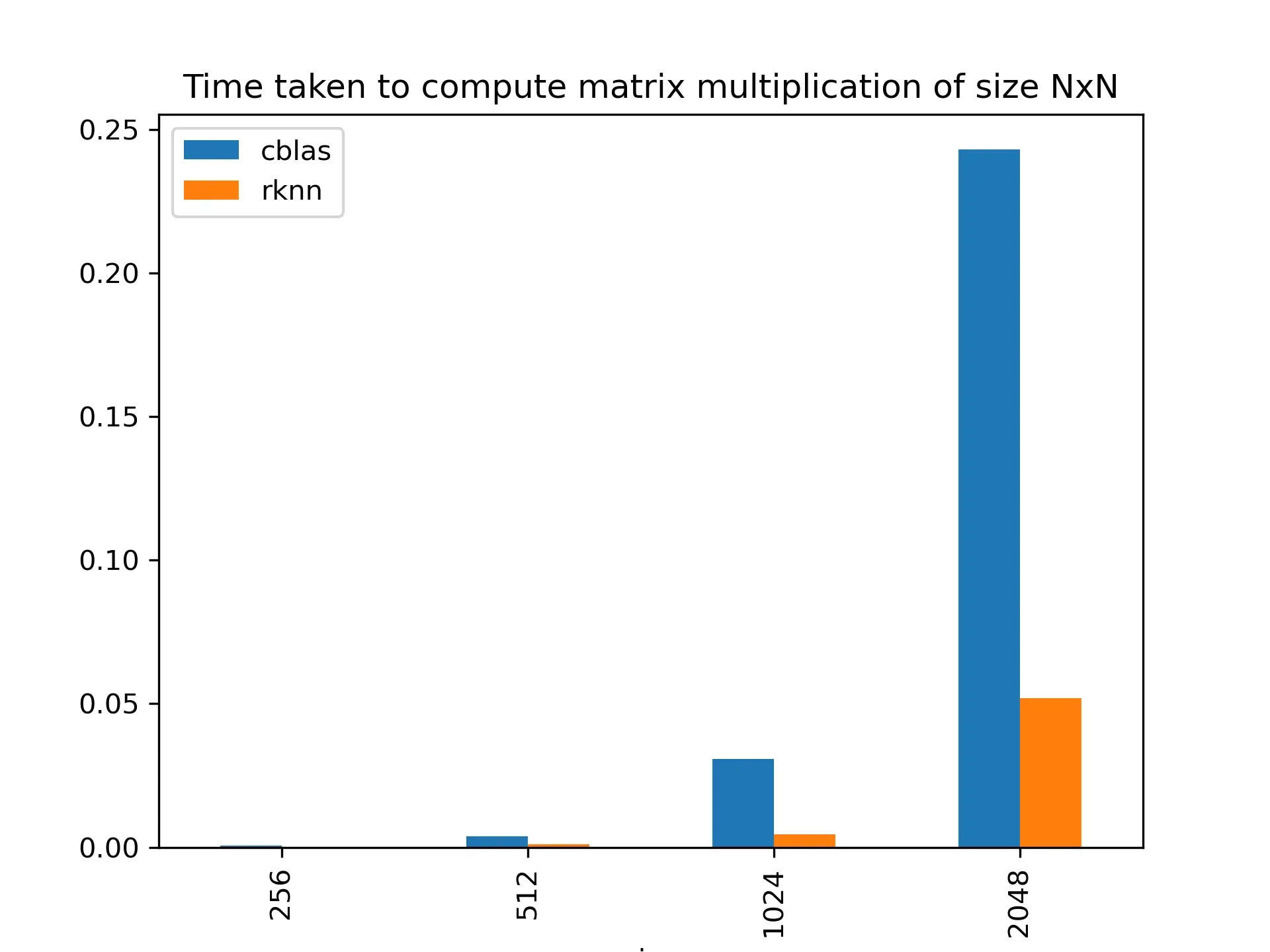
The source code can be found in the following link.