Adventuring into Tenstorrent SFPU Programming (Mandelbrot rendering)

After my previous post about Tenstorrent programming, I am curious about how exactly am I supposed to write my own LLK (programming the vector engine/SFPU). I tried it once back when I was still using Grayskull. Wanted to give it another try and see where I land. This time I set out to write a simple Mandelbrot renderer as the task is embarrassingly parallel and does not require complex cross-lane operations.

This post is more a "what I learned and how I did it" than a "how to" guide. The code far from optimal. And the source code is available on GitHub.

It is highly recommended to read my previous post about programming Tenstorrent devices and the expected programming model. Otherwise you won't understand a bit of what is going on.

In order to compare apples to apples. The CPU implementation is compiled with -march=native in order to utilize the full potential of the CPU. And is running on the following hardware:

• CPU: AMD EPYC 8124P (16 cores, 32 threads)
• RAM: 512GB DDR4
• Tenstorrent: Wormhole n300

The Mandelbrot set

First a recap on what the Mandelbrot set is. For our purposes, the Mandelbrot set is a set of complex numbers c for which the function f(z) = z^2 + c does not diverge when iterated from z = 0. That is, for all n in the natural numbers, the absolute value of f^n(0) remains bounded. And we can color the points in the complex plane based on how quickly the sequence diverges. For example, if the sequence does not diverge, we can color the point black. If the sequence diverges, we can color the point based on the iteration count.

The following will be baseline implementation. Which produces iterations as a vector of integers representing the number of iterations required for each pixel to diverge (or not, which the iteration count will equal to the max iteration count).

const size_t width = 1024;
const size_t height = 1024;

float left = -2.0f;
float right = 1.0f;
float bottom = -1.5f;
float top = 1.5f;

const int max_iteration = 64;

std::vector<int> iterations(width * height);
for(size_t y = 0; y < height; ++y) {
    for(size_t x = 0; x < width; ++x) {
        float real = left + (right - left) * x / (width - 1);
        float imag = bottom + (top - bottom) * y / (height - 1);

        float zx = real;
        float zy = imag;
        int iteration = 0;
        while(zx * zx + zy * zy < 4.0f && iteration < max_iteration) {
            float tmp = zx * zx - zy * zy + real;
            zy = 2.0f * zx * zy + imag;
            zx = tmp;
            ++iteration;
        }

        iterations[y * width + x] = iteration;
    }
}

Then the iteration count is converted into a color, here map_color mimics the color used by Ultra Fractal that everyone is the most familiar with. This separation is made to allow the accelerator kernel to focus on the iteration logic.

std::vector<uint8_t> image(width * height * 3);
for(size_t y = 0; y < height; ++y) {
    for(size_t x = 0; x < width; ++x) {
        int iteration = iterations[y * width + x];
        int max_iteration = 64;
        map_color((float)iteration/max_iteration, image.data() + y * width * 3 + x * 3);
    }
}

// Save the image
save_image("mandelbrot.png", width, height, 3, image.data(), width * 3);

Running this code produces a image of the Mandelbrot set:

Baseline implementation on a single Tensix core

Writing a SFPU program is not well documented by official resources. But manageable after some code reading and some trial and error. A great thanks to Corsix on the Tenstorrent Discord explaining a lot of the details about how the SFPU works. The official documentation sparse but combining it and lot of discussion reading, we can infer the SFPU on Wormhole:

• Is a 32-wide vector unit
• Capable of FP32 and UINT32 math operations
• Has internal registers called LReg and 7 of them is usable while the rest has special purpose
• Reads and writes to Dst registers which the unpacker and packer bring and carry data to and from the SFPU
• The SFPU is driven by the Math core (same as the FPU)

With the following diagram showing the general dataflow of the SFPU:

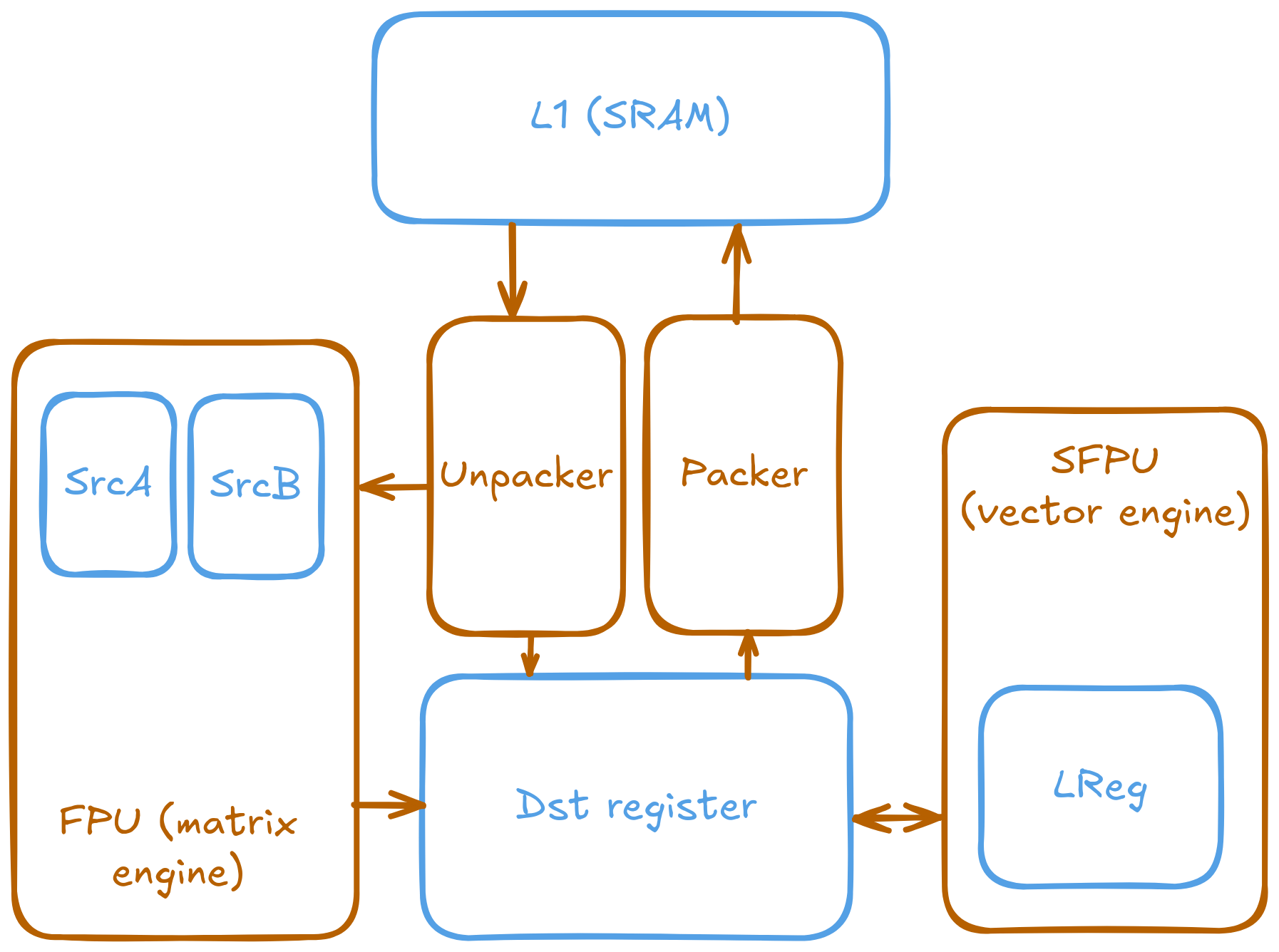
And the Tensix

• Operates on a tile (32x32 matrix) basis
• Needs explicit data movement between cores
• Requires synchronization between (compute) kernels
• Cores within Tensix act cooperatively
• Multiple Tensix can work cooperatively or using a SPMD pattern
• Not all Tensix needs to be running at the same time

The first implementation should be as simple as possible. We can model rendering a Mandelbrot as a complex binary operation (ba dum tss! get it? complex? both in not simple and complex numbers). The operator takes in two numbers, the real and imaginary parts of a complex number. Iterates through the quadratic formula. And spit out the iteration count of when it escapes. And the kernel shall only run on one Tensix. Core (0, 0) to be exact.

The code is based on my old vector addition example which now lives in the official tt-metal repository as a part of the contributed examples. It follows the typical Metalium flow. First, allocate 3 buffers. One for the real part, one for the imaginary part, and one for the output iteration count. Note that unlike most operations on Tenstorrent where operations are on a 32x32 matrix. I am going to abuse the fact that the SFPU is a vector unit and we are not going to use any cross lane operations, so it does not matter if the buffers are tilized or not; to make everything row major. Thus I can have my mind focus on writing the actual operation instead of tiling. At the cost of rows must have a size divisible by 1024 - even though the SFPU runs on 32 wide vectors. The packer and unpaker still sees a 32x32 matrix.

const float left = -2.0f;
const float right = 1.0f;
const float bottom = -1.5f;
const float top = 1.5f;
size_t width = 1024;
size_t height = 1024;

const uint32_t tile_size = TILE_WIDTH * TILE_HEIGHT;
if((width * height) % tile_size != 0)
    throw std::runtime_error("Invalid dimensions, width * height must be divisible by tile_size");
const uint32_t n_tiles = (width * height) / tile_size;
auto a = MakeBuffer(device, n_tiles, sizeof(float));
auto b = MakeBuffer(device, n_tiles, sizeof(float));
auto c = MakeBuffer(device, n_tiles, sizeof(float));

Then the buffers are filled with their respective real and imaginary parts then uploaded to the device.

std::vector<float> a_data(width * height); // Real plane
std::vector<float> b_data(width * height); // Imaginary plane

for(size_t y = 0; y < height; y++) {
    for(size_t x = 0; x < width; x++) {
        float real = left + (right - left) * x / width;
        float imag = bottom + (top - bottom) * y / height;
        a_data[y * width + x] = real;
        b_data[y * width + x] = imag;
    }
}

EnqueueWriteBuffer(cq, a, a_data, false);
EnqueueWriteBuffer(cq, b, b_data, false);

Setup create circular buffers to allow data to go from reader to compute to writer.

const CoreCoord core{0, 0};
CBHandle cb_a = MakeCircularBufferFP32(program, core, tt::CBIndex::c_0, tiles_per_cb);
CBHandle cb_b = MakeCircularBufferFP32(program, core, tt::CBIndex::c_1, tiles_per_cb);
CBHandle cb_c = MakeCircularBufferFP32(program, core, tt::CBIndex::c_16, tiles_per_cb);

Create the kernels and set their execution parameters. Execute it on devicve.

auto reader = CreateKernel(
    program,
    "../single_core/kernel/interleaved_tile_read.cpp",
    core,
    DataMovementConfig{.processor = DataMovementProcessor::RISCV_0, .noc = NOC::RISCV_0_default});
auto writer = CreateKernel(
    program,
    "../single_core/kernel/tile_write.cpp",
    core,
    DataMovementConfig{.processor = DataMovementProcessor::RISCV_1, .noc = NOC::RISCV_1_default});
auto compute = CreateKernel(
    program,
    "../single_core/kernel/mandelbrot_compute.cpp",
    core,
    ComputeConfig{.math_approx_mode = false, .compile_args = {}, .defines = {}});

SetRuntimeArgs(program, reader, core, {a->address(), b->address(), n_tiles});
SetRuntimeArgs(program, writer, core, {c->address(), n_tiles});
SetRuntimeArgs(program, compute, core, {n_tiles});

EnqueueProgram(cq, program, true);

Finally read the result back and do the same color mapping.

std::vector<float> c_data;
EnqueueReadBuffer(cq, c, c_data, true);
float* c_bf16 = reinterpret_cast<float*>(c_data.data());

std::vector<uint8_t> image(width * height * 3);
for(size_t y = 0; y < height; ++y) {
    for(size_t x = 0; x < width; ++x) {
        float iteration = c_bf16[y * width + x];
        constexpr int max_iteration = 64;
        map_color(iteration/max_iteration, image.data() + y * width * 3 + x * 3);
    }
}

save_image(image.data(), width, height, "mandelbrot_tt_single_core.png");

Kernel side. The data movement kernel is nearly the same as the data movement kernels in my previous article, besides from using FP32 instead of BFP16 (BFP16 is not accurate enough for this application). The reader takes 2 addresses and a count, reads from both addresses and feeds them into the circular buffer. The writer waits for the compute kernel to produce some results and writes them to DRAM.

// data read kernel (data movement kernel 0)
void kernel_main() {
    // Read parameters from the kernel arguments
    uint32_t a_addr = get_arg_val<uint32_t>(0);
    uint32_t b_addr = get_arg_val<uint32_t>(1);
    uint32_t n_tiles = get_arg_val<uint32_t>(2);

    const uint32_t tile_size_bytes = get_tile_size(cb_in0);

    const InterleavedAddrGenFast<true> a = {a_addr, tile_size_bytes, DataFormat::Float32};
    const InterleavedAddrGenFast<true> b = {b_addr, tile_size_bytes, DataFormat::Float32};

    for (uint32_t i = 0; i < n_tiles; i++) {
        cb_reserve_back(tt::c_1, 1);
        cb_reserve_back(tt::c_0, 1);
        noc_async_read_tile(get_write_ptr(tt::c_0), a, cb_in0_addr);
        noc_async_read_tile(get_write_ptr(tt::c_1), b, cb_in1_addr);

        noc_async_read_barrier();  // Wait until tile reads are done
        cb_push_back(tt::c_0, 1);
        cb_push_back(tt::c_1, 1);
    }
}

// data write kernel (data movement kernel 1)
void kernel_main() {
    uint32_t c_addr = get_arg_val<uint32_t>(0);
    uint32_t n_tiles = get_arg_val<uint32_t>(1);

    const uint32_t tile_size_bytes = get_tile_size(cb_out0);

    const InterleavedAddrGenFast<true> c = {c_addr, tile_size_bytes, DataFormat::Float32};

    for (uint32_t i = 0; i < n_tiles; i++) {
        cb_wait_front(tt::c_16, 1);
        noc_async_write_tile(get_read_ptr(tt::c_16), c, cb_out0_addr);
        noc_async_write_barrier();
        cb_pop_front(tt::c_16, 1);
    }
}

Now the fun part. To implement the compute kernel. Since it is a elementwise binary operation. The input and output from the compute kernel is the same as the original vector addition, that part is solved. But how about the SFPU kernel itself? Official documentation is not super helpful as it simply tells us what a LLK (SFPU operation) looks like, and what it has access to. Without saying how data gets in and out of the SFPU kernel. See the following link (which happens to be the only documented LLK):

* Constants are expressed as scalars but are expanded to the width of the vector
* v_if (and related) predicate execution of vector operations such that only enabled vector elements are written
* The compiler views v_if and v_elseif as straight-line code, ie, both sides of the conditionals are executed
* RISCV conditional and looping instructions work as expected (only one side executed)
* Math expressions for vectors work across all enabled vector elements
* Presently, v_endif is required to close out all v_if/v_elseif/v_else chains

void silly(bool take_abs)
{
    // dst_reg[n] loads into a temporary LREG
    vFloat a = dst_reg[0] + 2.0F;

    // This emits a load, move, mad (on GS uses the "+/0 .5" feature of MAD)
    dst_reg[3] = a * -dst_reg[1] + vConst0p6929 + 0.5F;

    // This emits a load, loadi, mad (a * dst_reg[] goes down the mad path)
    dst_reg[4] = a * dst_reg[1] + 1.2F;

    // This emits two loadis and a mad
    dst_reg[4] = a * 1.5F + 1.2F;

    // This emits a loadi (into tmp), loadi (as a temp for 1.2F) and a mad
    vFloat tmp = s2vFloat16a(value);
    dst_reg[5] = a * tmp + 1.2F;

    v_if ((a >= 4.0F && a < 8.0F) || (a >= 12.0F && a < 16.0F)) {
        vInt b = exexp_nodebias(a);
        b &= 0xAA;
        v_if (b >= 130) {
            dst_reg[6] = setexp(a, 127);
        }
        v_endif;
    } v_elseif (a == s2vFloat16a(3.0F)) {
        // RISCV branch
        if (take_abs) {
            dst_reg[7] = abs(a);
        } else {
            dst_reg[7] = a;
        }
    } v_else {
        vInt exp = lz(a) - 19;
        exp = ~exp;
        dst_reg[8] = -setexp(a, exp);
    }
    v_endif;
}

We can infer SFPU kernels can do full lane predication/masking. Like how GPUs do. But the Math RISC-V core is still driving the SFPU. Thus care must be taken about when to branch on the RISC-V and when to branch (mask) on the SFPU. And there are certain constants stored in hardware registers that can be used at all times.

Since reading the friendly manuals is not enough. Then it's time to read the source code.

Looking into the SFPU add operation and using it as a reference. It's a long chain of calls eventually calling _calculate_sfpu_binary_ which we finally see the real vector operation. ITERATIONS seems to be a magic number set to 8. I assume this is some convention used by llk_math_eltwise_binary_sfpu_params in order to overlap unpacking and math.

ALWI void add_binary_tile(uint32_t idst0, uint32_t idst1) {
    MATH((llk_math_eltwise_binary_sfpu_binop<APPROX, ckernel::sfpu::BinaryOp::ADD>(idst0, idst1)));
}

template <bool APPROXIMATE, ckernel::sfpu::BinaryOp BINOP>
inline void llk_math_eltwise_binary_sfpu_binop(uint dst_index0, uint32_t dst_index1, int vector_mode = VectorMode::RC) {
    llk_math_eltwise_binary_sfpu_params<APPROXIMATE>(
        ckernel::sfpu::calculate_sfpu_binary<APPROXIMATE, BINOP>, dst_index0, dst_index1, vector_mode);
}

template <bool APPROXIMATION_MODE, BinaryOp BINOP, int ITERATIONS = 8>
inline void calculate_sfpu_binary(const uint dst_offset) {
    _calculate_sfpu_binary_<APPROXIMATION_MODE, BINOP, ITERATIONS>(dst_offset);
}

template <bool APPROXIMATION_MODE, BinaryOp BINOP, int ITERATIONS = 8>
inline void _calculate_sfpu_binary_(const uint dst_offset)
{
    // SFPU microcode
    for (int d = 0; d < ITERATIONS; d++)
    {
        constexpr uint dst_tile_size = 32;
        sfpi::vFloat in0             = sfpi::dst_reg[0];
        sfpi::vFloat in1             = sfpi::dst_reg[dst_offset * dst_tile_size];
        sfpi::vFloat result          = 0.0f;
        if constexpr (BINOP == BinaryOp::ADD)
        {
            result = in0 + in1;
        }
        ...
        sfpi::dst_reg[0] = result;
        sfpi::dst_reg++;
    }
}

I came up with the following, mimicking the operator tenstorrent have written and keeping the same magic numbers. It grabs the real and imaginary parts of the complex number and iterates the quadratic formula. If the resulting point is a radius of 2. Then the iteration counter is incremented. Then the iteration counter is saved to the destination register. Note the real part and result occupies the same register, thus the result will overwrite the original value. This is intentional and seems to be the convention by official LLKs.

Also note the ifdef to limit the code to be compiled only on the Math core. The other cores (unpack, pack) does not have the necessary headers included to compile this code. Nor it's their job issuing vector instrustions.

#ifdef TRISC_MATH
#define ITERATIONS (8)
inline void mandelbrot(const uint dst_offset) {
  constexpr uint dst_tile_size = 32;
  for(int _=0;_<ITERATIONS;_++) {
    vFloat real = dst_reg[0];
    vFloat imag = dst_reg[dst_offset * dst_tile_size];
    vFloat zx = real;
    vFloat zy = imag;
    vFloat count = 0;

    constexpr int max_iter = 64;
    for(int i=0;i<max_iter;i++) {
      v_if(zx * zx + zy * zy < 4.f) {
        vFloat tmp = zx * zx - zy * zy + real;
        zy = 2.f * zx * zy + imag;
        zx = tmp;
        count += 1.f;
      }
      v_endif;
    }
    dst_reg[0] = count;
    dst_reg++;
  }
}
#endif

Executing the custom LLK can be done via the same llk_math_eltwise_binary_sfpu_params wrapper function. The MATH macro isolates the invocation to only the math core and not the pack and unpacker.

namespace NAMESPACE {
void MAIN {
    uint32_t n_tiles = get_arg_val<uint32_t>(0);

    constexpr auto cb_in0 = tt::CBIndex::c_0;
    constexpr auto cb_in1 = tt::CBIndex::c_1;
    constexpr auto cb_out0 = tt::CBIndex::c_16;

    init_sfpu(cb_in0, cb_out0);
    add_binary_tile_init();
    for (uint32_t i = 0; i < n_tiles; i++) {
            // Wait for reader to have data ready
            cb_wait_front(cb_in0, 1);
            cb_wait_front(cb_in1, 1);
            // Make sure we have SFPU register ready to use
            tile_regs_acquire();
            tile_regs_wait();
            // Unpack data from input buffers into SFPU registers (called dst registers)
            copy_tile(cb_in0, 0, 0);
            copy_tile(cb_in1, 0, 1);
            // Remove the used data from input buffers so reader can read next data
            cb_pop_front(cb_in0, 1);
            cb_pop_front(cb_in1, 1);

            // invoke mandelbrot function
            // pseudo code: dst[0] = mandelbrot(dst[0], dst[1]);
            MATH(llk_math_eltwise_binary_sfpu_params<false>(mandelbrot, 0, 1, VectorMode::RC);)

            // store result in output buffer
            cb_reserve_back(cb_out0, 1);
            pack_tile(0, cb_out0);
            // commit the tile to the output buffer
            tile_regs_commit();
            tile_regs_release();
            // send the tile to the output buffer
            cb_push_back(cb_out0, 1);
    }
}
}

Mechanically copying how LLks for legit worked! Producing near identical results as the CPU render. Quick benchmarking shows this SFPU kernel version only slightly slower than the CPU (both under single thread!). Which is actually not bad considering the Wormhole runs at 1GHz compared to the CPU's 3GHz max boost. And the SFPU not being the focus of the architecture.

Settings: max iteration = 64, image size = 1024x1024

CPU (single core): 0.0453537s
SFPU (single core): 0.0476342s

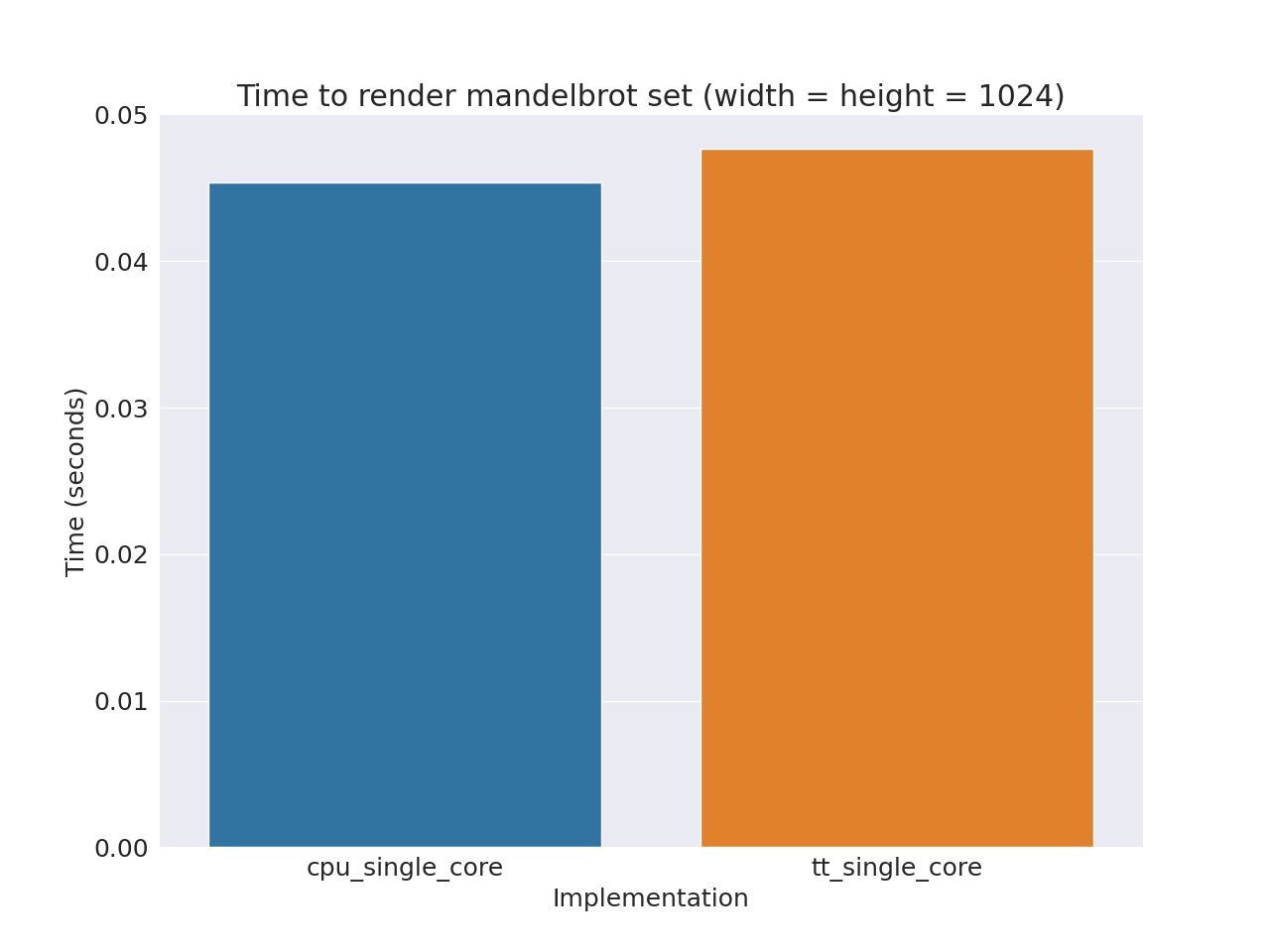
Generating the complex field on SFPU

The obvious thing to do next is to not have the complex field stored in DRAM and let the SFPU generate it on the fly. It's cheating to let the CPU to do the job, upload the entire buffer and not count it towards the actual execution time. I am unsure if this is really optimization or not though. As rendering the Mandelbrot set is a computationally intensive task and thus memory should not the bottleneck.

SFPU lane patterns

One thing Corsix talked about on Discord was how the SFPSTORE instruction skips a lane when going form lreg (SFPU internal register) to dst (shared register between SFPU and packer). I am unsure why it is made this way though.

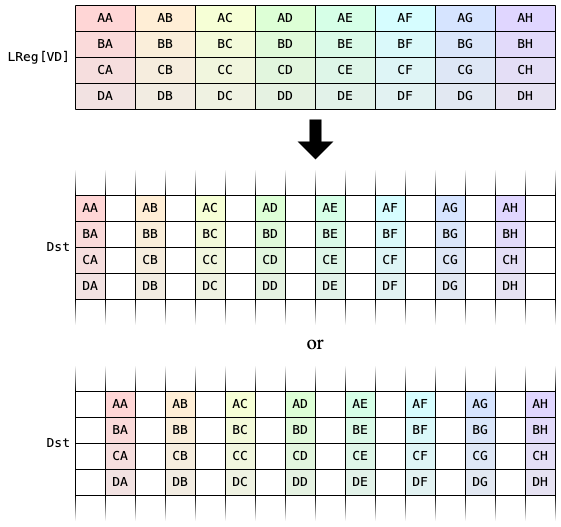
Keeping this in mind, we can replace the above mandelbrot function with simple linear generator and get rid of the reader kernel. That leaves us with simply the writer and modified compute. Also looking at llk_math_eltwise_binary_sfpu_params, some setup is needed to prepare the dst registers for writing. vConstTileId on Wormhole is a special variable that holds the line ID (multiplied by 2!); containing [0, 2, 4... 64]. It is the only way to know which lane a variable is on.

#ifdef TRISC_MATH
inline void mandelbrot() {
    math::set_dst_write_addr<DstTileLayout::Default, DstTileShape::Tile32x32>(0);
    math::set_addr_mod_base();
    TTI_STALLWAIT(p_stall::STALL_SFPU, p_stall::MATH);

    // Since we are handling the SFPU invocation directly without the help of wrappers
    // Now we need to iterate 32 times as that maps to the number of vector in a tile
    // Luckly we picked max iteration to be 64, so a difference of 1 is still visible
    // in the final output
    for(int i=0; i<32;i++) {
        vFloat out = int32_to_float(i);
        dst_reg[i] = out;
    }

    math::clear_dst_reg_addr();
    TTI_STALLWAIT(p_stall::STALL_CFG, p_stall::WAIT_SFPU);
    math::clear_addr_mod_base();
}

#endif

namespace NAMESPACE {
void MAIN {

    ....
    for(uint32_t y = 0; y < height; y++) {
        float y_coord = bottom + (top - bottom) * y / height;
        for(uint32_t x = 0; x < width / (TILE_WIDTH * TILE_HEIGHT); x += 1) {
            // Deleted code related to taking input
            tile_regs_acquire();
            tile_regs_wait();

            // Now we directly invoke the SFPU
            MATH(mandelbrot());

            cb_reserve_back(cb_out0, 1);
            pack_tile(0, cb_out0);
            tile_regs_commit();
            tile_regs_release();
            cb_push_back(cb_out0, 1);
        }
    }
}
}

Run and zoom into the output. We indeed see a striped pattern of 1 in difference. This is actually a problem. As most vector programming assumes lanes next to each other in the register will result in lanes being adjacent in memory/final output. And it's not in the SFPU.

Wiring the actual LLK

This is the final LLK. I had to duplicate the code and handle the even and odd vectors separately as the compiler does not like me doing anything with lane calculations and broadcasting the results into every lane. The idea is still simple though. The function takes three arguments: y_coord, left, and right. It vectorizes across the width of the image, 1024 elements at a time. From imag=y_coord and real from left to right. Otherwise it is the same core calculation.

Stupid? yes. It works? hell yeah!

inline void mandelbrot(float y_coord, float left, float right) {
    math::set_dst_write_addr<DstTileLayout::Default, DstTileShape::Tile32x32>(0);
    math::set_addr_mod_base();
    TTI_STALLWAIT(p_stall::STALL_SFPU, p_stall::MATH);

    float lane_delta = (right - left) / 1024.f;
    constexpr int max_iter = 64;
    float lane_offset = 0.0f;
    // HACK: Split the even and odd iterations because SFPU does interleaved foramt (for some reason)
    for(int i=0;i<32;i+=2) {
        vFloat vleft = left;
        vFloat vright = right;
        vFloat vi = int32_to_float(i / 2);
        vFloat vdelta = vright - vleft;
        vFloat vchunk_coarse = vleft + (vdelta) * (1.f / 16.f) * vi;
        vFloat vreal_lane_id = int32_to_float(vConstTileId);
        vFloat vchunk_fine = vchunk_coarse + (vreal_lane_id) * lane_delta;

        vFloat real = vchunk_fine;
        vFloat imag = y_coord;
        vFloat zx = real;
        vFloat zy = imag;
        vFloat count = 0;

        for(int i=0;i<max_iter;i++) {
          v_if(zx * zx + zy * zy < 4.f) {
            vFloat tmp = zx * zx - zy * zy + real;
            zy = 2.f * zx * zy + imag;
            zx = tmp;
            count += 1.f;
          }
          v_endif;
        }
        dst_reg[i] = count;
    }

    for(int i=1;i<32;i+=2) {
        vFloat vleft = left;
        vFloat vright = right;
        vFloat vi = int32_to_float(i / 2);
        vFloat vdelta = vright - vleft;
        vFloat vchunk_coarse = vleft + (vdelta) * (1.f / 16.f) * vi;
        vFloat vreal_lane_id = int32_to_float(vConstTileId+1);
        vFloat vchunk_fine = vchunk_coarse + (vreal_lane_id) * lane_delta;

        vFloat real = vchunk_fine;
        vFloat imag = y_coord;
        vFloat zx = real;
        vFloat zy = imag;
        vFloat count = 0;

        for(int i=0;i<max_iter;i++) {
          v_if(zx * zx + zy * zy < 4.f) {
            vFloat tmp = zx * zx - zy * zy + real;
            zy = 2.f * zx * zy + imag;
            zx = tmp;
            count += 1.f;
          }
          v_endif;
        }
        dst_reg[i] = count;
    }

    math::clear_dst_reg_addr();
    TTI_STALLWAIT(p_stall::STALL_CFG, p_stall::WAIT_SFPU);
    math::clear_addr_mod_base();
}

The compiler crashlog if I try lane calculations:

Failed to generate binaries for mandelbrot_compute TT_THROW @ /home/marty/Documents/tt/tt-metal/tt_metal/jit_build/build.cpp:66: tt::exception
info:
trisc1 build failed. Log: during RTL pass: rvtt_replay
/home/marty/Documents/tt/tt-metal//tt_metal/hw/firmware/src/trisck.cc: In function 'kernel_launch':
/home/marty/Documents/tt/tt-metal//tt_metal/hw/firmware/src/trisck.cc:67:1: internal compiler error: in find_writer, at config/riscv/tt/rtl-rvtt-replay.cc:142
   67 | }
      | ^
0x1350669 diagnostic_impl(rich_location*, diagnostic_metadata const*, int, char const*, __va_list_tag (*) [1], diagnostic_t)
	???:0
0x135154e internal_error(char const*, ...)
	???:0
0x5ec992 fancy_abort(char const*, int, char const*)
	???:0
0x5dd0a5 find_writer(int, rtx_insn const*) [clone .cold]
	???:0
0xe4049d (anonymous namespace)::pass_rvtt_replay::execute(function*)
	???:0
Please submit a full bug report, with preprocessed source (by using -freport-bug).
Please include the complete backtrace with any bug report.
See <https://github.com/tenstorrent/sfpi> for instructions.

Performance wise this is worse then the previous implementation that touches DRAM. Not unexpected as previously field calculation was left out of the measurement. And in this version, we are asking the RSIC-V, which does not have a floating-point unit, to perform the a little bit of floating point during loop setup. Which is slow (any why most cores have hardware floating-point math, not on Tensix, the hardware floating point only does vector and matrix operations).

The following graph shows the performance of the new algorithm called "nullary". Meaning the LLK does not take input. As in, trinary, binary, unary, and nullary (which I named myself).

Settings: max iteration = 64, image size = 1024x1024

CPU (single core): 0.0453537s
SFPU (single core): 0.0476342s
SFPU (single core, nullary): 0.0500179

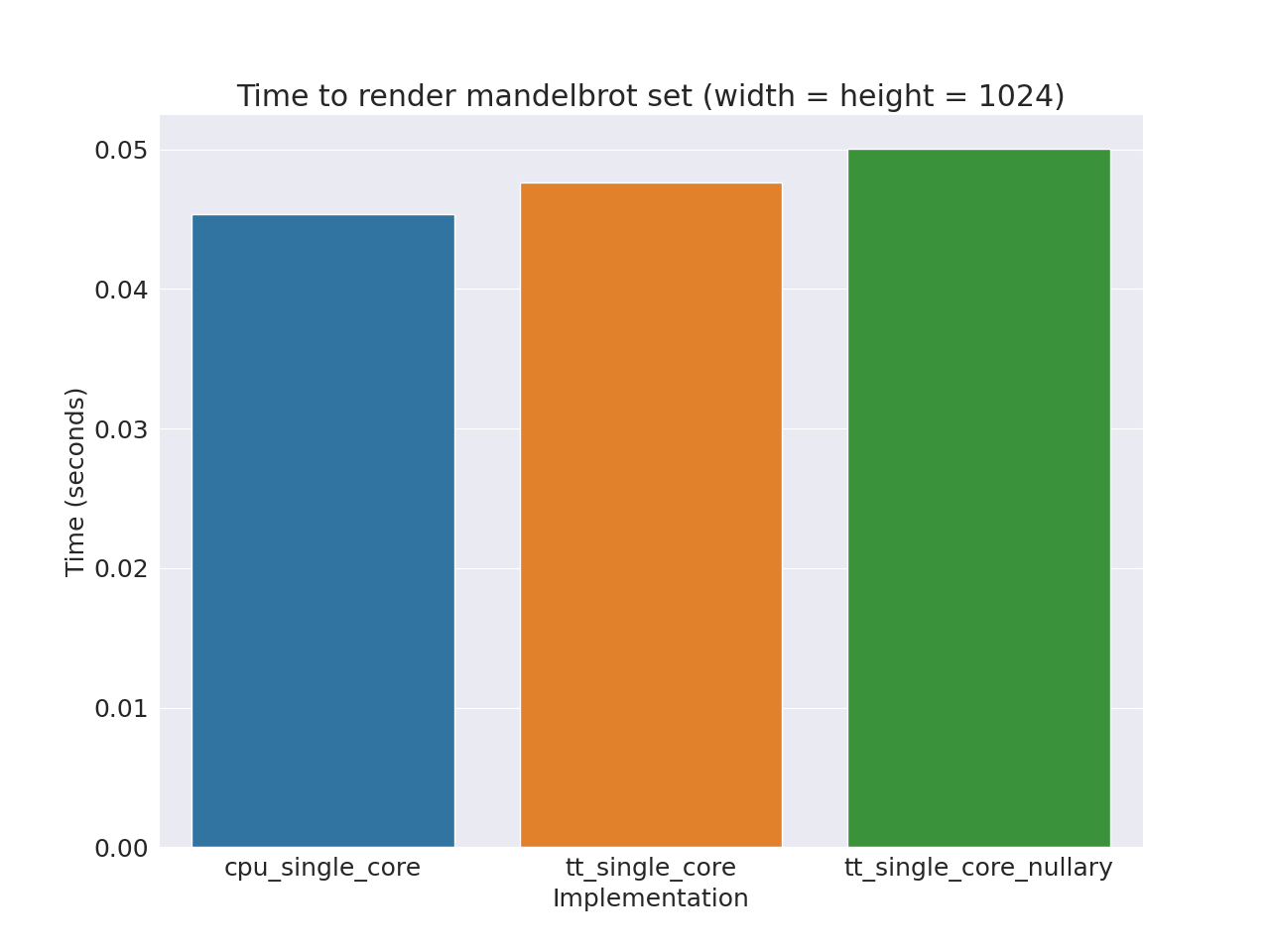
Parallelizing across all cores

Now we shall attempt to utilize all cores and beat the CPU in speed. Unlike OpenCL where scaling across cores is trivial, Metalium although gives you infrastructure to do so. It is a job of the developer to setup the correct configuration, writing your own SPMD program, and executing it in parallel across all cores. This inconvenience is flexibility showing. As Metalium also allows MPMD that fully utilizes the systolic nature of the architecture.

First step, instead of creating the kernels for a single core, we create it across all cores. Likewise for circular buffers

auto core_grid = device->compute_with_storage_grid_size();
auto all_cores = CoreRange({0, 0}, {core_grid.x - 1, core_grid.y - 1});

auto writer = CreateKernel(
    program,
    "../multi_core_nullary/kernel/tile_write.cpp",
    all_cores,
    DataMovementConfig{.processor = DataMovementProcessor::RISCV_1, .noc = NOC::RISCV_1_default});
auto compute = CreateKernel(
    program,
    "../multi_core_nullary/kernel/mandelbrot_compute.cpp",
    all_cores,
    ComputeConfig{.math_approx_mode = false, .compile_args = {}, .defines = {}});

CBHandle cb_c = MakeCircularBufferFP32(program, all_cores, tt::CBIndex::c_16, tiles_per_cb);

Next modify both the writer and compute kernels allow it to only process a subset of the problem. Here we split it naturally along the height dimension.

// data movement kernel (writer)
void kernel_main() {
    uint32_t c_addr = get_arg_val<uint32_t>(0);
    uint32_t start_row = get_arg_val<uint32_t>(1);    // new!
    uint32_t end_row = get_arg_val<uint32_t>(2);      // new!
    uint32_t tiles_per_row = get_arg_val<uint32_t>(3);// new!
    ...
    for (uint32_t i = start_row * tiles_per_row; i < end_row * tiles_per_row; i++) {
        ...
    }

// compute kernel
namespace NAMESPACE {
void MAIN {
    constexpr uint32_t TILE_WIDTH = 32;
    constexpr uint32_t TILE_HEIGHT = 32;
    float left = get_arg_val<float>(0);
    float right = get_arg_val<float>(1);
    float bottom = get_arg_val<float>(2);
    float top = get_arg_val<float>(3);
    uint32_t width = get_arg_val<uint32_t>(4);
    uint32_t height = get_arg_val<uint32_t>(5);
    uint32_t start_row = get_arg_val<uint32_t>(6);   // new!
    uint32_t end_row = get_arg_val<uint32_t>(7);     // new!

    ..
    for(uint32_t y = start_row; y < end_row; y++) {             // only work on  the sub problem
        float y_coord = bottom + (top - bottom) * y / height;   // calculate y coordinate
        for(uint32_t x = 0; x < tiles_per_row; x += 1) {
        ...
        }
    }
}
}

Then for each core in the chip. Give them a different subproblem to solve (different starting row and ending row).

uint32_t num_cores = core_grid.x * core_grid.y;
uint32_t height_chunk = height / num_cores + (height % num_cores != 0);
for(uint32_t i=0; i<num_cores; ++i) {
    uint32_t x = i % core_grid.x;
    uint32_t y = i / core_grid.x;
    CoreCoord core(x, y);

    uint32_t start_row = i * height_chunk;
    uint32_t end_row = std::min(start_row + height_chunk, uint32_t(height));

    SetRuntimeArgs(program, writer, core, {c->address(), start_row, end_row, uint32_t(width / tile_size)});
    SetRuntimeArgs(program, compute, core, {params[0], params[1], params[2], params[3], uint32_t(width), uint32_t(height), start_row, end_row});
}

And run! It works! Now it is MUCH faster! Even faster than the CPU on all cores! Now even comparing to the CPU on all cores, using OpenMP. It is a small bar compared to the skyscraper of the CPU.

Settings: max iteration = 64, image size = 1024x1024

CPU (single core): 0.0453537s
SFPU (single core): 0.0476342s
SFPU (single core, nullary): 0.0500179
SFPU (all (56) cores, nullary): 0.000911271
CPU (all (32) threads): 0.0204544

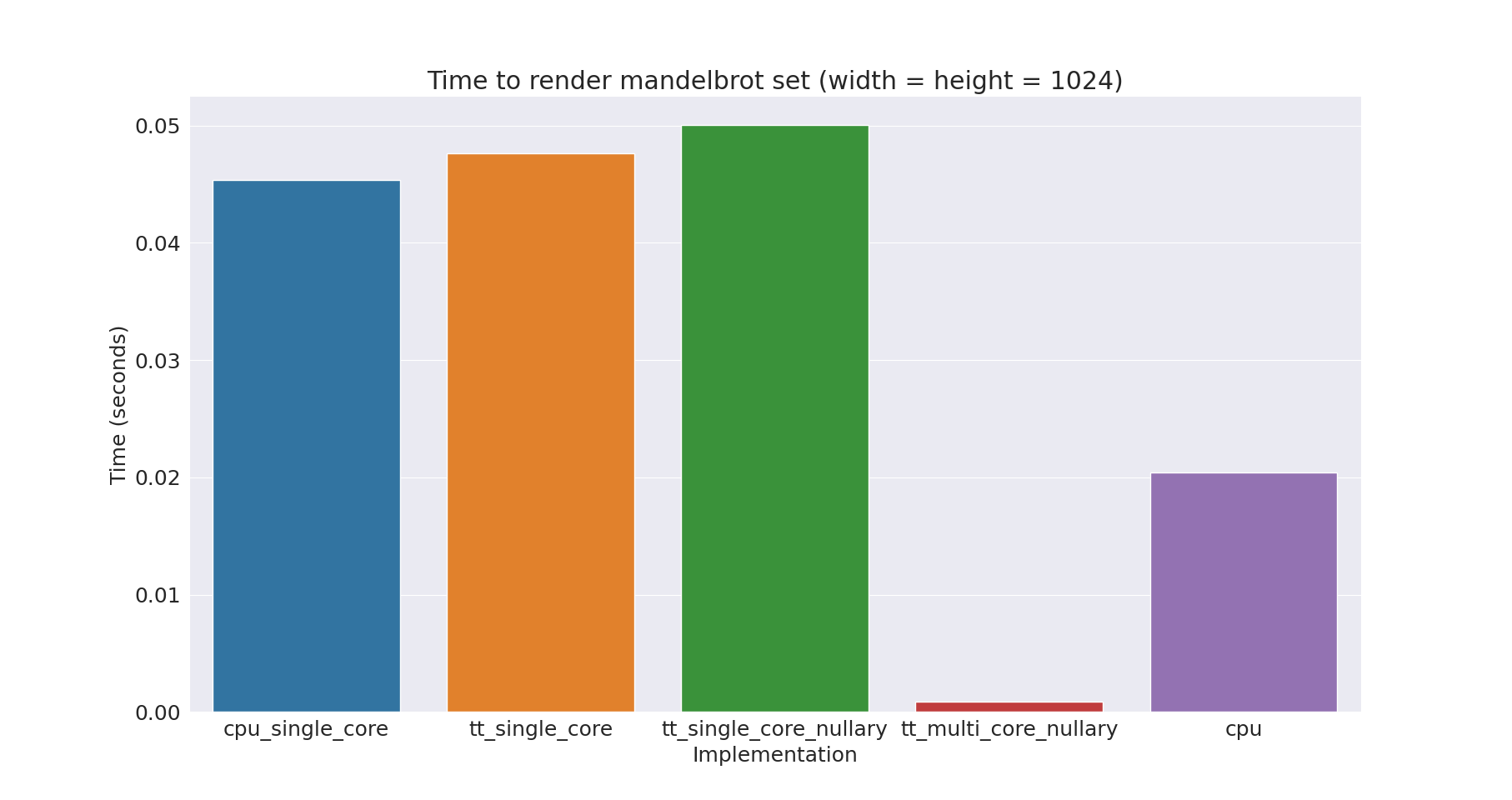
More benchmarking

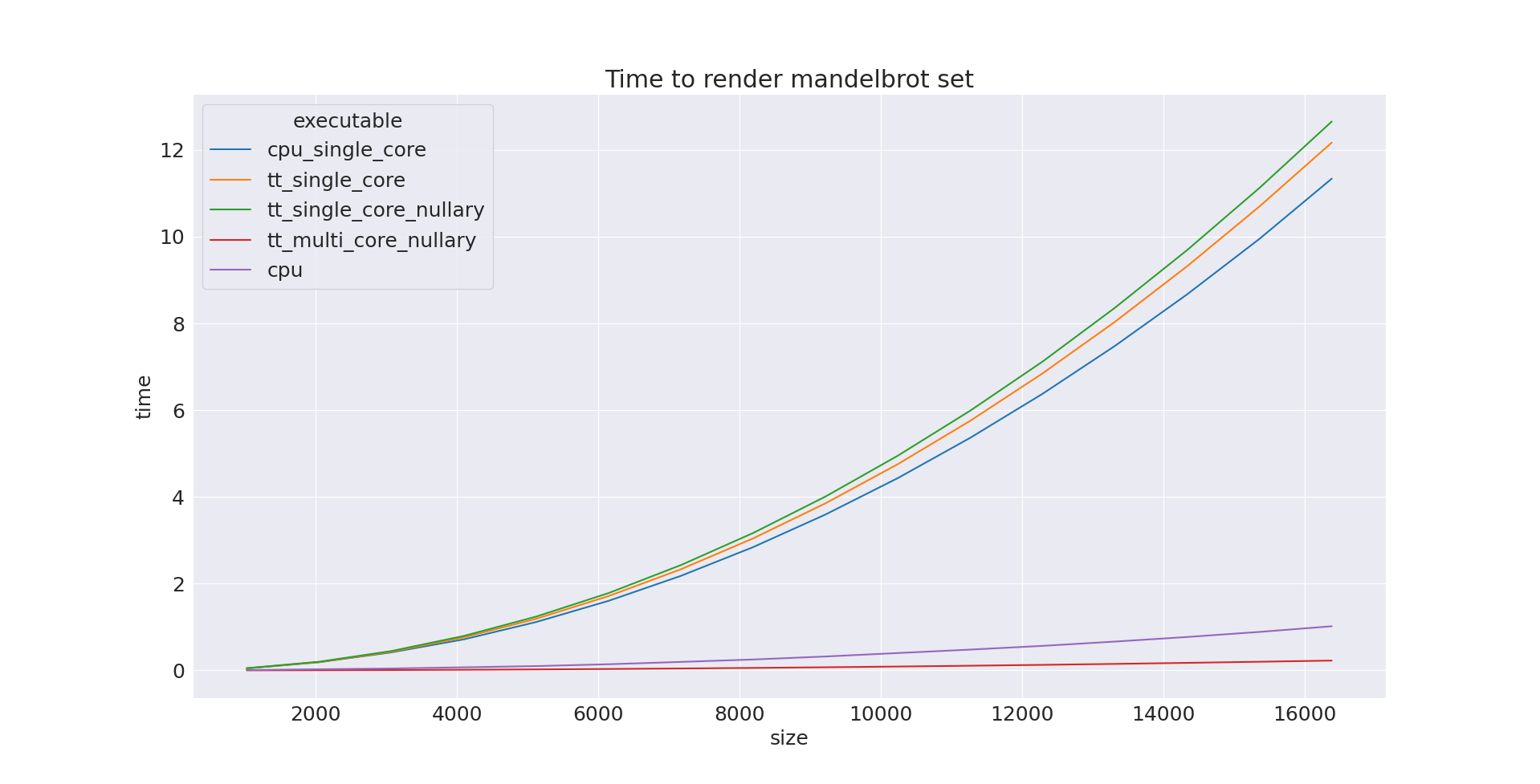
I explored the performance of the different algorithms by rendering the Mandelbrot at various resolutions. The result, shown in the following plot, shows that the SFPU implementation utilizing all cores outperforms the CPU by a factor of 4.5. While it is not GPU-level performance, it is still great considering the hardware's main design is for AI workloads, not general-purpose computing. I am abusing the hardware. Plus there's another Wormhole chip on the n300. And this is far from optimized code.

See that the parallel SFPU line be basically flat!

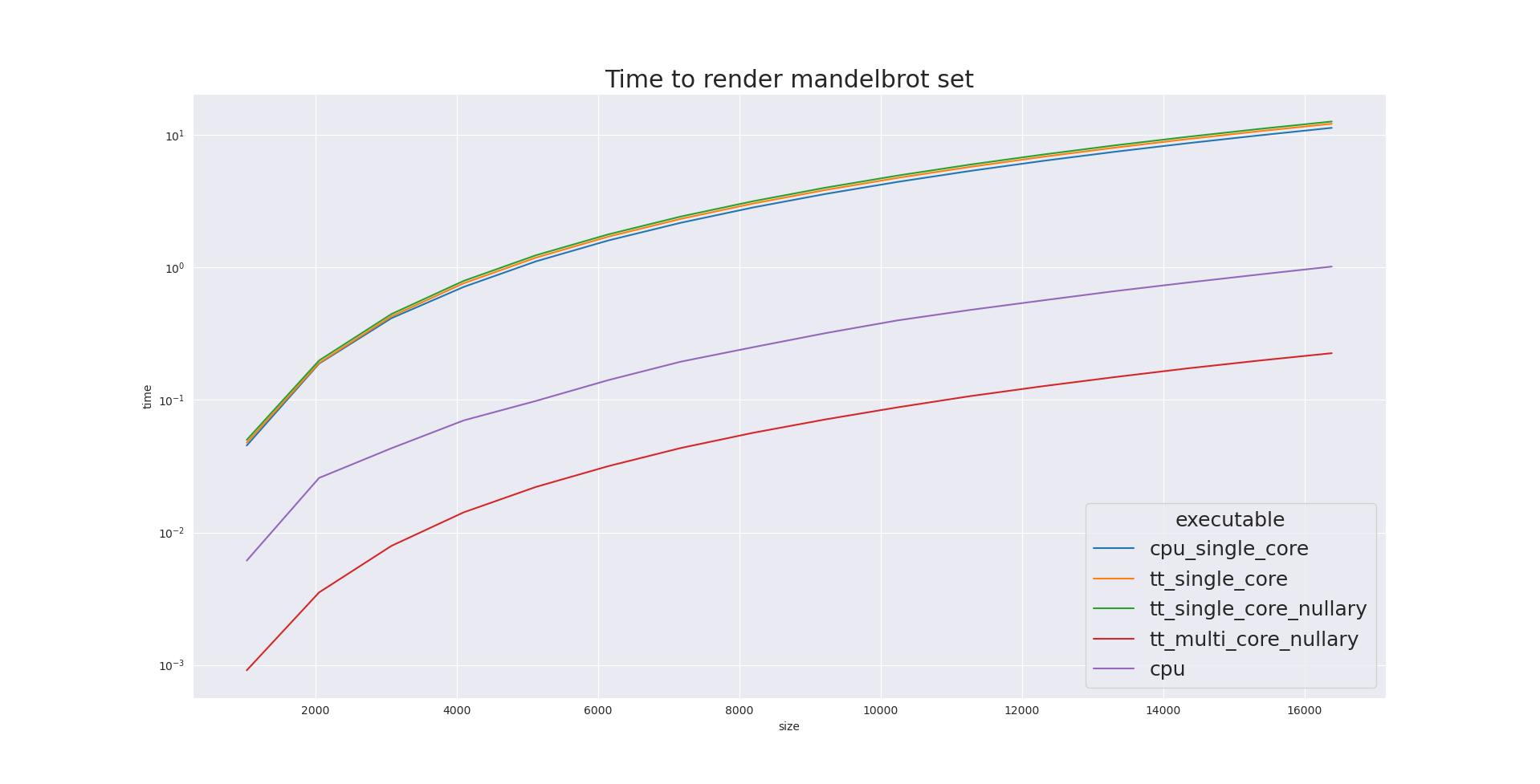
The log plot is also very beautiful, showing the problem is truly compute bound and problem size does not suddenly increase due to cache effects (only for the CPU, Tenstorrent does not have a cache).

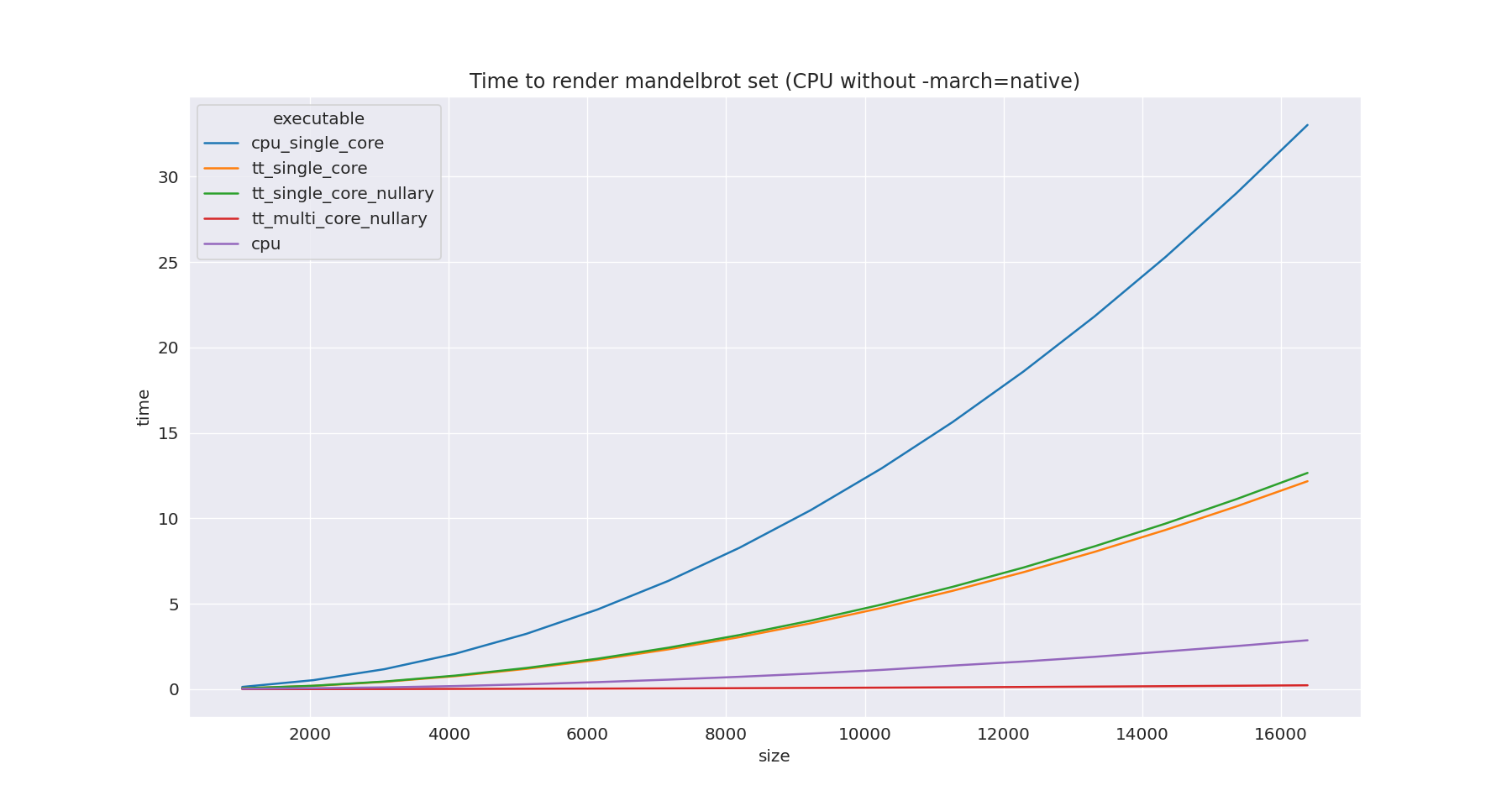
Compared to CPU without the-march=native flag, the multicore SFPU implementation is about 12.6x faster then CPU multicore. Now the CPU line is really flat.

Gallery

Mandelbrot set rendered on Tenstorrent Wormhole. Size 2048x2048. Kernel execution time: 0.0036655s

Mandelbrot set rendered on Tenstorrent Wormhole. Size 2048x2048. Rnage x: [0.4, 0.45], y: [-0.25, -0.2]

Hope this long winded rambling is helpful to someone. Peronsally I feel like programming LLKs is like controlling a massive processor by coding as if it is an embedded system. It's insane, but also very fun and I see to potential to push out every ounce of performance.