Building the RoPE operation for Tenstorrent hardware

Rotary Position Embedding, or RoPE is a critical operations used in Large Language Models. Responsible of encoding positional information (where the token is in the sentence) into the embedding, so the model can distinguish between "the cat eats the bird" and "bird eats the cat". Ever since my journey starting to add a Tenstorrent backend into GGML. RoPE has always been falling back to the CPU. As TTNN although have it's own RoPE implementation, is fundamentally incompatible with the semantics GGML wants. I have been putting off writing my own RoPE support as I expect it to be a pain and hoping someone would Deus Ex Machina and give me a working version in a PR out of no where.

To say, I was wrong. I improved the Tenstorrent GGML backend to the degree where RoPE support is now the main bottleneck for inference performance. What else can I do.. Time to get my hand dirty.

IMPORTANT: As you can see looking at the right hand side - the scrollbar on this page - the post is VERY long. I do not have the energy nor space to guide you through the entire process. The raw Gemtext file of this post is about 117KB! And I wrote every word.

It is assumed that the reader have a very solid understanding of parallel computing patterns, computer organization, hardware architecture and imagination to interpret the gaps.

I hope this blog post can serve as a reference in the future for "how the stuff works" and if software vendors are interested in Tensotrrent's processors, how to program them.

Source code (the NeoX variant) available in the following link (licsned under Zero-Clause BSD):

And the acual integration lives in my llama.cpp fork. Kernels linked below

RoPE

I highly recommend my friend Fleetwood's blog on the mathematics and design philosophy of RoPE.

Done? Good. I am not mathematician and my barin goes blank as soon as I see complicated equations. Let's decompose RoPE into computation:

• For each RoPE operation. A vector and a position value is provided.
• For each pair of values in the vector
• Define i as the index of the first element (of the pair) in the vector and D being the size of the vector
• Calculate the frequency of rotation = 1 / 10000^(i / D)
• Calculate rotation angle = position * frequency
• Apply a 2D rotation of angle angle to the pair

I choose to implement the NeoX variant of RoPE as that seems easier. It splits the entire vector into 2 halfs. Then rotate pairwise between the 2 vectors.

std::vector<float> rope(const std::vector<float>& vec, int pos)
{
    size_t D = vec.size();
    assert(D % 2 == 0 && "Dimension must be even");
    std::vector<float> result(D);
    for (size_t i = 0; i < D/2; ++i) {
        float exponent = 2.0f * i / D ;
        float freq = 1.0f / std::pow(10000.0f, exponent);

        // Calculate the angle of rotation
        float angle = pos * freq;
        float cos_angle = std::cos(angle);
        float sin_angle = std::sin(angle);

        // Calculate the rotation matrix
        float cos_sin = cos_angle * sin_angle;
        float sin_cos = sin_angle * cos_angle;

        // Apply the rotation to the pair
        float x = vec[i];
        float y = vec[i + D/2];

        result[i] = x * cos_angle - y * sin_angle;
        result[i + D/2] = x * sin_angle + y * cos_angle;
    }

    return result;
}

Really simple isn't it? The mechanisms are clear as soon as you're not looking at vectorized equations.

Additionally, we ought to support multiple vectors in a single operation (denoted N here). If you look into GGML's API. It sometimes wants to limit how many dimensions RoPE is applied. So new parameters are introduced. D denotes the width of the input data (vec.size() == D * N and D_active denotes the number of dimensions the operation is applied to. The following implementation can be derived:

std::vector<float> rope(const std::vector<float>& vec, const std::vector<int>& pos, int D, int D_active)
{
    size_t rotate_dim = D_active == -1 ? vec.size() : D_active;
    assert(D_active % 2 == 0 && "Active dimension must be even");
    assert(D_active <= D && "Active dimension must be less than or equal to total dimension");
    std::vector<float> result(vec.size());
    size_t n = pos.size();
    for(size_t n = 0; n < N; ++n) {
        size_t offset = n * D;
        for (size_t i = 0; i < D_active/2; i ++) {
            float exponent = 2.f * (float)i / D_active;
            float freq = 1.0f / std::pow(10000.0f, exponent);

            float angle = pos * freq;
            float cos_angle = std::cos(angle);
            float sin_angle = std::sin(angle);

            float x = vec[offset + i];
            float y = vec[offset + i + D_active/2];

            result[offset + i] = x * cos_angle - y * sin_angle;
            result[offset + i + D_active/2] = x * sin_angle + y * cos_angle;
        }

        for (size_t i = D_active; i < D; i++) {
            result[offset + i] = vec[offset + i];
        }
    }
    return result;
}

We can check our implementation against GGML using with some simple coding:

// GGML
int main(void) {
    const int D = 32;
    const int N = 1;
    std::vector<float> input_vec(D * N);
    for(int i = 0; i < D * N; i++) {
        input_vec[i] = (float)i;
    }
    std::vector<int> pos(N);
    for(int i = 0; i < N; i++) {
        pos[i] = i+1;
    }

    // Arbitrary amount of allowed memory as the example is small
    size_t ctx_size = 5 * 1024 * 1024; // 5 MB

    struct ggml_init_params params = {
        /*.mem_size   =*/ ctx_size,
        /*.mem_buffer =*/ NULL,
        /*.no_alloc   =*/ false,
    };
    struct ggml_context * ctx = ggml_init(params);

    struct ggml_tensor * tensor_a = ggml_new_tensor_2d(ctx, GGML_TYPE_F32, D, N);
    struct ggml_tensor * tensor_b = ggml_new_tensor_2d(ctx, GGML_TYPE_I32, N, 1);
    memcpy(tensor_a->data, input_vec.data(), ggml_nbytes(tensor_a));
    memcpy(tensor_b->data, pos.data(), ggml_nbytes(tensor_b));


    struct ggml_cgraph * gf = ggml_new_graph(ctx);

    struct ggml_tensor * result = ggml_rope(ctx, tensor_a, tensor_b, D/2, GGML_ROPE_TYPE_NEOX);
    ggml_build_forward_expand(gf, result);
    ggml_graph_compute_with_ctx(ctx, gf, 1);

    // Print result
    float * result_data = (float *) result->data;
    for(size_t i = 0; i < N; i++) {
        printf("vector %zu:\n", i);
        for(size_t j = 0; j < D; j++) {
            printf("%f ", result_data[i * D + j]);
        }
        printf("\n");
    }

    ggml_free(ctx);
}

// Ours
int main() {
    constexpr size_t D = 32;
    std::vector<float> vec(D);
    for(size_t i = 0; i < D; ++i) {
        vec[i] = i;
    }

    auto res = rope(vec, 1, D/2);
    for (size_t i = 0; i < res.size(); ++i) {
        std::cout << res[i] << (i < res.size() - 1 ? ", " : "\n");
    }
}

Which prints

GGML:
-6.731768 -1.848437 0.991674 2.650707 3.879802 4.958866 5.985997 6.995256 4.322418 8.864721 10.149709 11.089353 12.039399
13.015746 14.005993 15.002213 16.000000 17.000000 18.000000 19.000000 20.000000 21.000000 22.000000 23.000000 24.000000
25.000000 26.000000 27.000000 28.000000 29.000000 30.000000 31.000000

Ours:
-6.73177, -1.84844, 0.991674, 2.65071, 3.8798, 4.95887, 5.986, 6.99526, 4.32242, 8.86472, 10.1497, 11.0894, 12.0394, 13.0157,
14.006, 15.0022, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31

Good - we have a working reference and mental model now.

Implementing RoPE

Let's understand some design constraint before diving into code. RoPE is not a trival element wise operation, in two differnt ways

• The heavy but predictable use of sin() and cos()
• Running RoPE requires knowledge of which element in the vector is being processed

sin() and cos() are expensive to compute - no surprise there. Most backends dodge this by precomputing the values on the host, dumping them into device DRAM as a "sin/cos cache," and then just indexing into that at runtime. Since the inputs are always the same for a given set of hyperparameters, this works fine. But not on Tenstorrent. Here, everything runs in tiles, so I'd have to write a gather just to pull the right values from DRAM, and then hack up the data movement kernel to handle sub-tile access (forget about using helpers like TensorAccessor or InterleavedAddressGen{,Fast} - they won't know what to do). This design would be forbiddingly difficult to write. So, trigonometric functions have to be computed on the fly.

With that said, some amount of manual addressing is still required. Especially as it will be required to extract the position index in order to apply it across the entire vector later on.

I recommend reviewing the Metalium Programming Model guide if you are not familare with it already. As it will serve as the base knowledge assumed in this post.

RoPE also needs each pair of elements to be rotated by a different amount, based on their index. So, which element lands in which SFPU lane actually matters (RoPE is not a simple element wise operation), and the internal format of a tile must be taken into account. The official documentations (I wrote most of them :p) should help with understanding:

And my previous experiment programming the SFPU (though disregarding the tile structure at the time) would also be an interesting read for readers into weird programming practices.

For a baseline, the kernel could run on a single (Tensix) core, utilizing the SFPU (vector engine) and supporting RoPE on part of the input tensor (the n_dims mentioned earlier, a hard requirement by GGML). I'll simplify things by skipping the need to read varying token positions from an integer tensor and instead apply a single value across all vectors. It's easier this way, and loading an array of integers later should be straightforward enough.

Implementation strategy

Let's visualize the input vector. There's an active and passive region, the active reagon is where RoPE will be performed on, and is splitted subsequently into 2 euqal sized subreagons. Which are then iterated together pairwise to perform the actual calculation. The passive reagon is simply not touched.

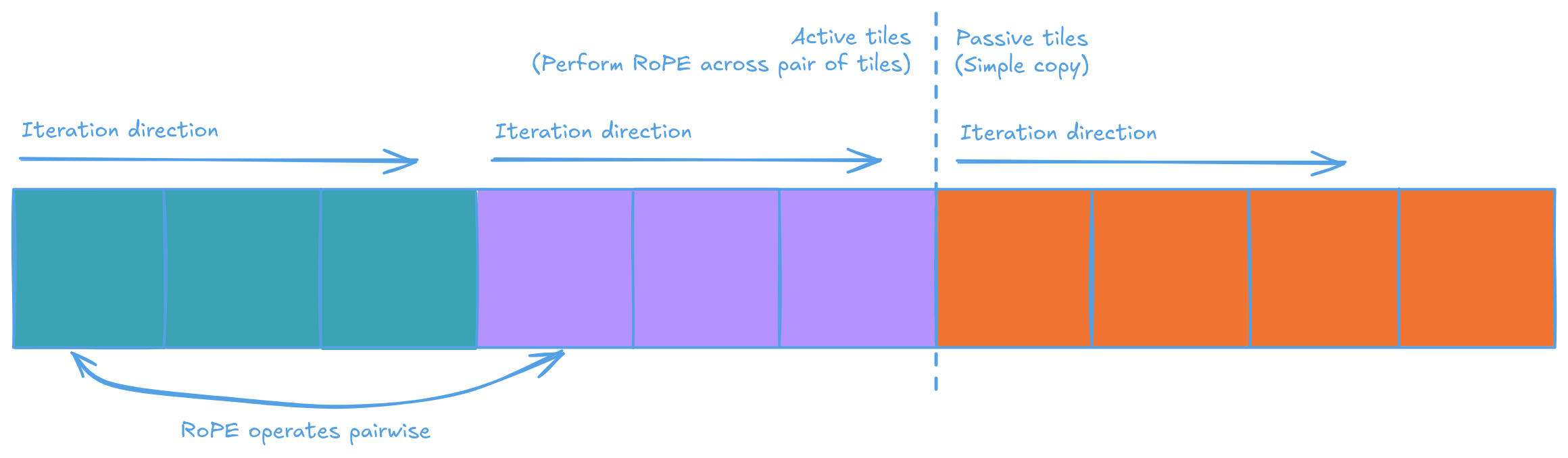
In the active region, where RoPE will performed. We:

• split the active region into two halves
• Data Movement kernel 0 (DM0) moves a tile from each half into the input Circular Buffer, transferring to the compute kernel
• Compute kernel moves the tiles into Dst registers
• Performs RoPE using the SFPU, against data on the Dst registers
• Store result back onto the Dst registers
• Move result to the output Circular Buffer
• Data Movement kernel 1 (DM1) moves the result back into DRAM
• Repeat until all active tiles are processed

The following diagram illustrates the flow of processing active tiles:

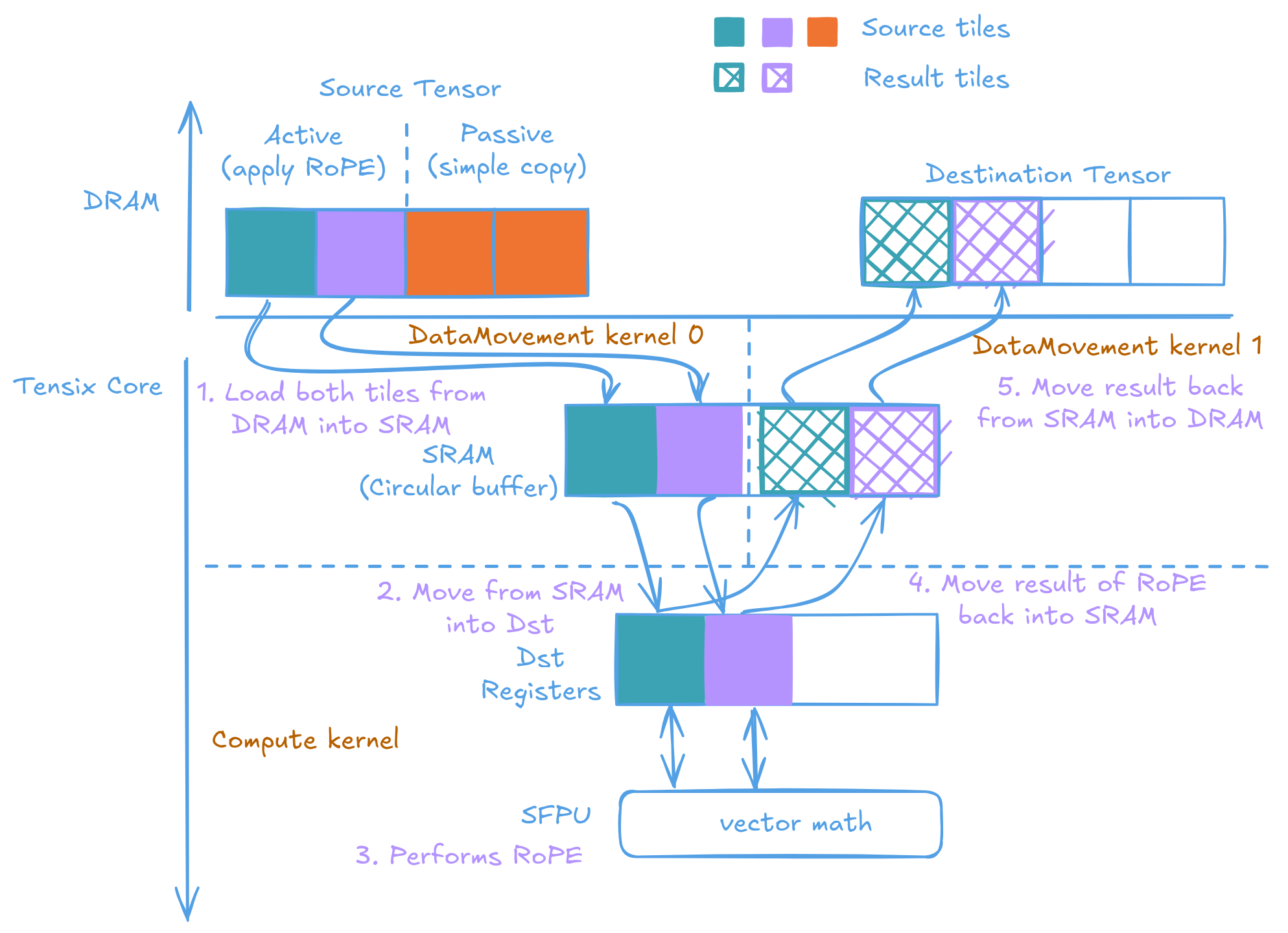
NOTE: The diagram only shows one pair of active tiles due to space constraints. In real-world scenarios, you'll typically encounter multiple pairs of active tiles within a single row.

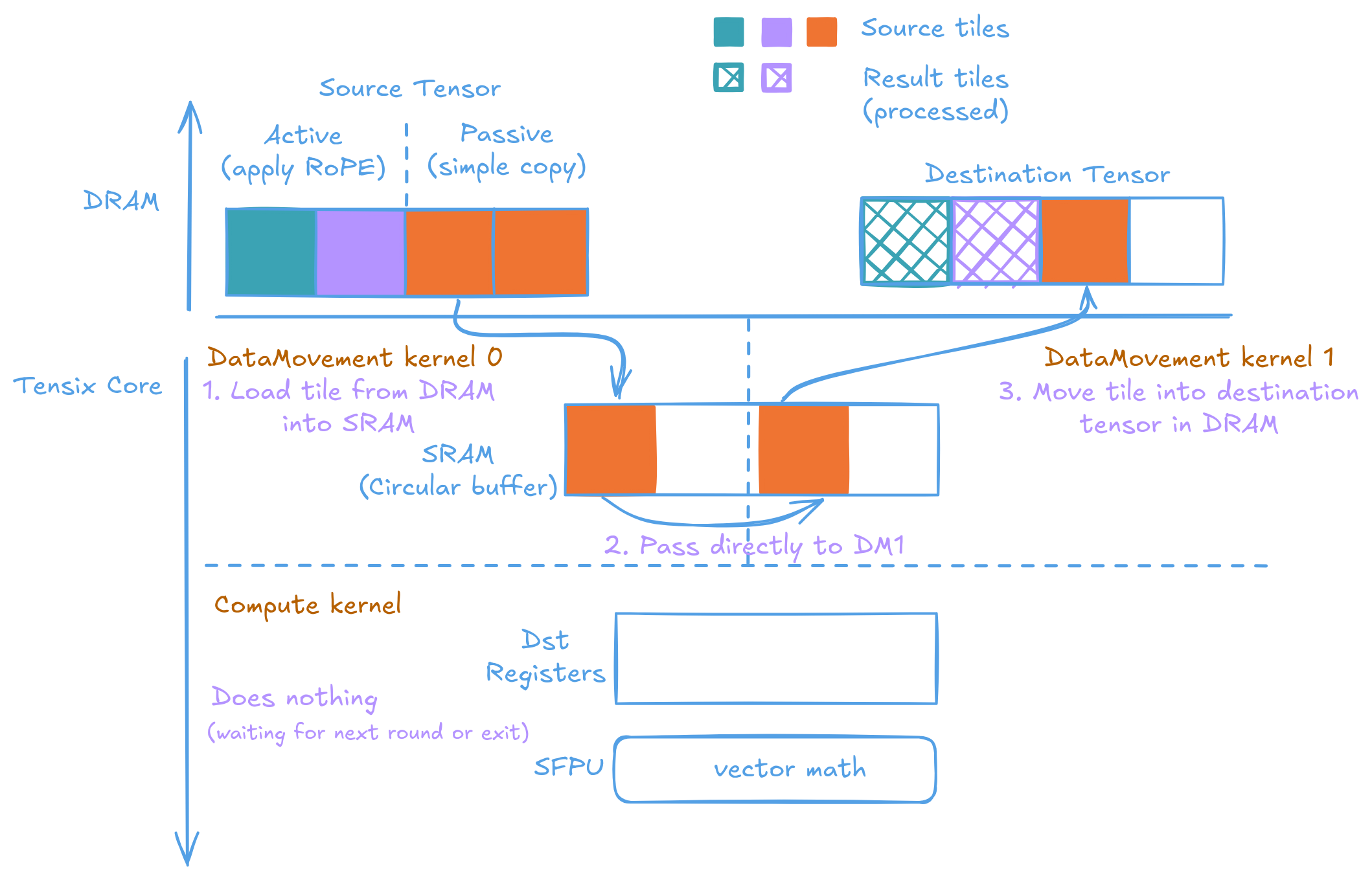
After all active tiles are processed, the kernel switch to processing passive tiles. In this phase, the compute kernel is effectively disabled, waiting for the next round (if available). Data Movement kernel 0 directly passes the input tile to Data Movement kernel 1 for writing out into the result tensor. Arguably it could be more efficient if it directly write the passive tiles into the result tensor from Data Movement kernel 0. But I consider that too much of a complication for too little benifit.

To set things up. On the host side (I have written some wrappers to make the Metalium API easier to use):

constexpr size_t D = 64;          // Length of the vector
constexpr size_t D_active = 64;   // Active reagon size
constexpr size_t N = 32;          // "Batch" size

// The above variables in number tiles
constexpr uint32_t Dt = D/32;
constexpr uint32_t Nt = N/32;
constexpr uint32_t D_activet = D_active/32;

// Buffers for input and output
auto src = MakeBuffer(device, Dt * Nt, sizeof(float));
auto dst = MakeBuffer(device, Dt * Nt, sizeof(float));

// The 3 citcular buffers for data passing
MakeCircularBufferFP32(program, core, tt::CBIndex::c_0, 4);  // Data into the compute kernel (reader/DM0 -> Compute)
MakeCircularBufferFP32(program, core, tt::CBIndex::c_16, 4); // Data out of compute kernel (Compute -> writer/DM1)
MakeCircularBufferFP32(program, core, tt::CBIndex::c_17, 4); // Moves passive tiles (reader/DM0 -> writer/DM1)

The reader implemts the reading part of our stradegy. Read the pairs of ative tiles and send to compute. Then read the passive tiles and send to writer

// Runtime kernel parameters
uint32_t src_addr = get_arg_val<uint32_t>(0);
uint32_t n_tiles_width_active = get_arg_val<uint32_t>(1);
uint32_t n_tiles_width = get_arg_val<uint32_t>(2);
uint32_t n_tiles_height = get_arg_val<uint32_t>(3);

const uint32_t tile_size_bytes = get_tile_size(cb_in0);
const auto src = TensorAccessor(TensorAccessorArgs<0>(), src_addr, tile_size_bytes);

constexpr uint32_t cb_in0 = tt::CBIndex::c_0;
constexpr uint32_t cb_bypass = tt::CBIndex::c_17;

for(uint32_t h = 0; h < n_tiles_height; h++) {
    // Reads the active tile pairs and send them to the compute kernel
    for(uint32_t w = 0; w < n_tiles_width_active/2; w++) {
        uint32_t tile_idx = h * n_tiles_width + w;
        uint32_t tile_idx2 = h * n_tiles_width + (w + n_tiles_width_active/2);

        cb_reserve_back(cb_in0, 2);
        uint32_t cb_src_addr = get_write_ptr(cb_in0);
        noc_async_read_tile(tile_idx, src, cb_src_addr);
        noc_async_read_tile(tile_idx2, src, cb_src_addr + tile_size_bytes);
        noc_async_read_barrier();
        cb_push_back(cb_in0, 2);
    }

    // Reads the passive tiles and forward to writer
    for(uint32_t w = n_tiles_width_active; w < n_tiles_width; w++) {
        uint32_t tile_idx = h * n_tiles_width + w;

        cb_reserve_back(cb_bypass, 1);
        noc_async_read_tile(tile_idx, src, get_write_ptr(cb_bypass));
        noc_async_read_barrier();
        cb_push_back(cb_bypass, 1);
    }
}

Compute is where the complexity lives. The kernel itself is as straightforward and as typical as it is - wait for 2 tiles, move them into Dst. Do math. Move them from Dst back into Circular Buffer. Loop.

uint32_t n_tiles_width_active = get_arg_val<uint32_t>(0);
uint32_t n_tiles_width = get_arg_val<uint32_t>(1);
uint32_t n_tiles_height = get_arg_val<uint32_t>(2);

constexpr uint32_t cb_in0 = tt::CBIndex::c_0;
constexpr uint32_t cb_out0 = tt::CBIndex::c_16;

init_sfpu(tt::CBIndex::c_0, tt::CBIndex::c_16);
for(uint32_t i = 0; i < n_tiles_height; i++) {
    for(uint32_t j = 0; j < n_tiles_width_active/2; j++) {
        cb_wait_front(cb_in0, 2);
        tile_regs_acquire();
        copy_tile_init(cb_in0);
        copy_tile(cb_in0, 0, 0);
        copy_tile(cb_in0, 1, 1);
        MATH(rope_tile(1000, n_tiles_width_active*32, j*32));
        tile_regs_commit();
        tile_regs_wait();

        cb_reserve_back(cb_out0, 2);
        pack_reconfig_data_format(cb_out0);
        pack_tile(0, cb_out0, 0);
        pack_tile(1, cb_out0, 1);
        tile_regs_release();
        cb_push_back(cb_out0, 2);
        cb_pop_front(cb_in0, 2);
    }
}

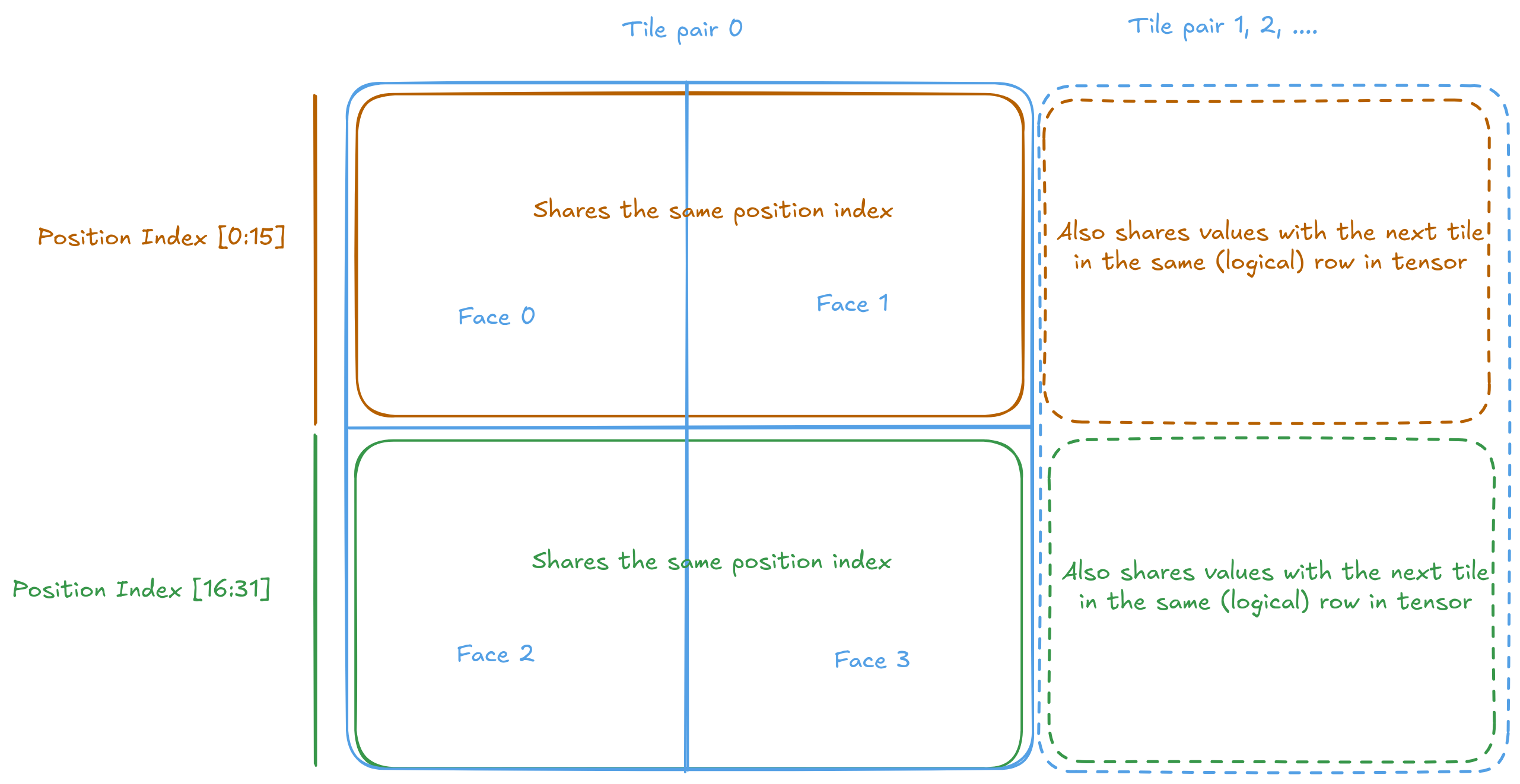
The tricky part lies in the custom rope_tile function. Remember (and if you don’t, go read the documentation on Tiles - shame on you and your cow for skipping it) that each tile is made up of 4 faces, with each face being a 16x16 row-major matrix. rope_tile configures the SFPU - don’t ask me what exactly it does; I borrowed the setup from elsewhere, and it just works - and then runs the actual computation 4 times, once for each face.

inline void rope_tile(int pos, int D_active, int vec_offset)
{
    math::set_dst_write_addr<DstTileLayout::Default, DstTileShape::Tile32x32>(0);
    math::set_addr_mod_base();
    TTI_STALLWAIT(p_stall::STALL_SFPU, p_stall::MATH);

    for (int face = 0; face < 4; face++) {
        rope_face(pos, D_active, vec_offset + ((face % 2 == 0) ? 0 : 16)); // real work happens here!
        TTI_SETRWC(p_setrwc::CLR_NONE, p_setrwc::CR_D, 8, 0, 0, p_setrwc::SET_D);
        TTI_SETRWC(p_setrwc::CLR_NONE, p_setrwc::CR_D, 8, 0, 0, p_setrwc::SET_D);
    }

    math::clear_dst_reg_addr();
    TTI_STALLWAIT(p_stall::STALL_CFG, p_stall::WAIT_SFPU);
    math::clear_addr_mod_base();
}

rope_face handles the actual computation. Implementing it is quite the journey. The first challenge is accessing different tiles stored via copy_tile. Tiles are spaced 32 dst_reg apart. The TTI commands in the caller function adjust the pointer so that each call begins at the start of a new face. To access the same chunk on another tile, simply add 32 to the current index.

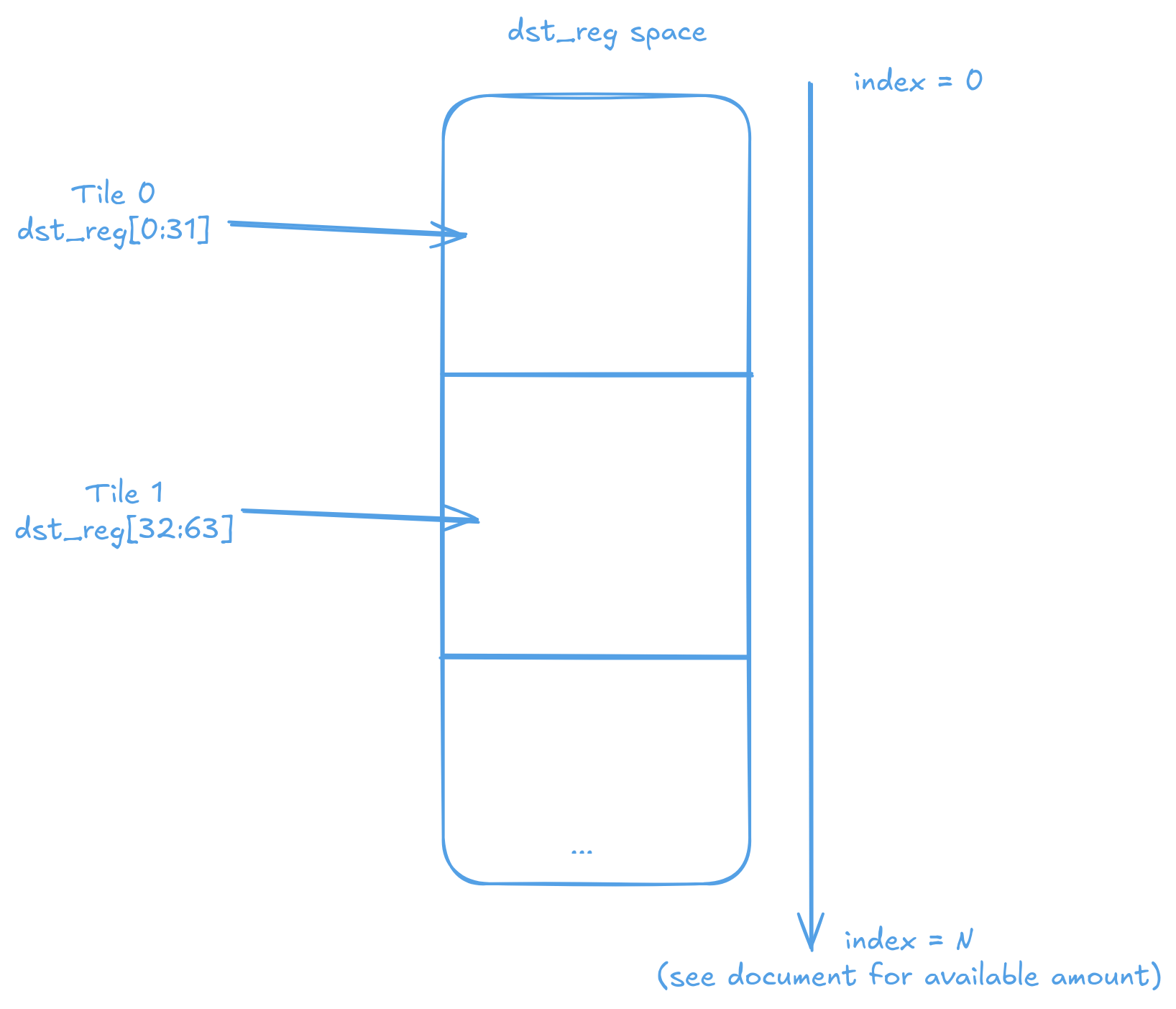
And how are the faces loaded into the SFPU? You might expect that since the SFPU is 32-wide and each face has a width of 16, each load would simply bring in 2 rows into the SFPU. That is not the case. For some reason (well, there's legit reasons, but will not get into that here) the load is interleaved in Dst.

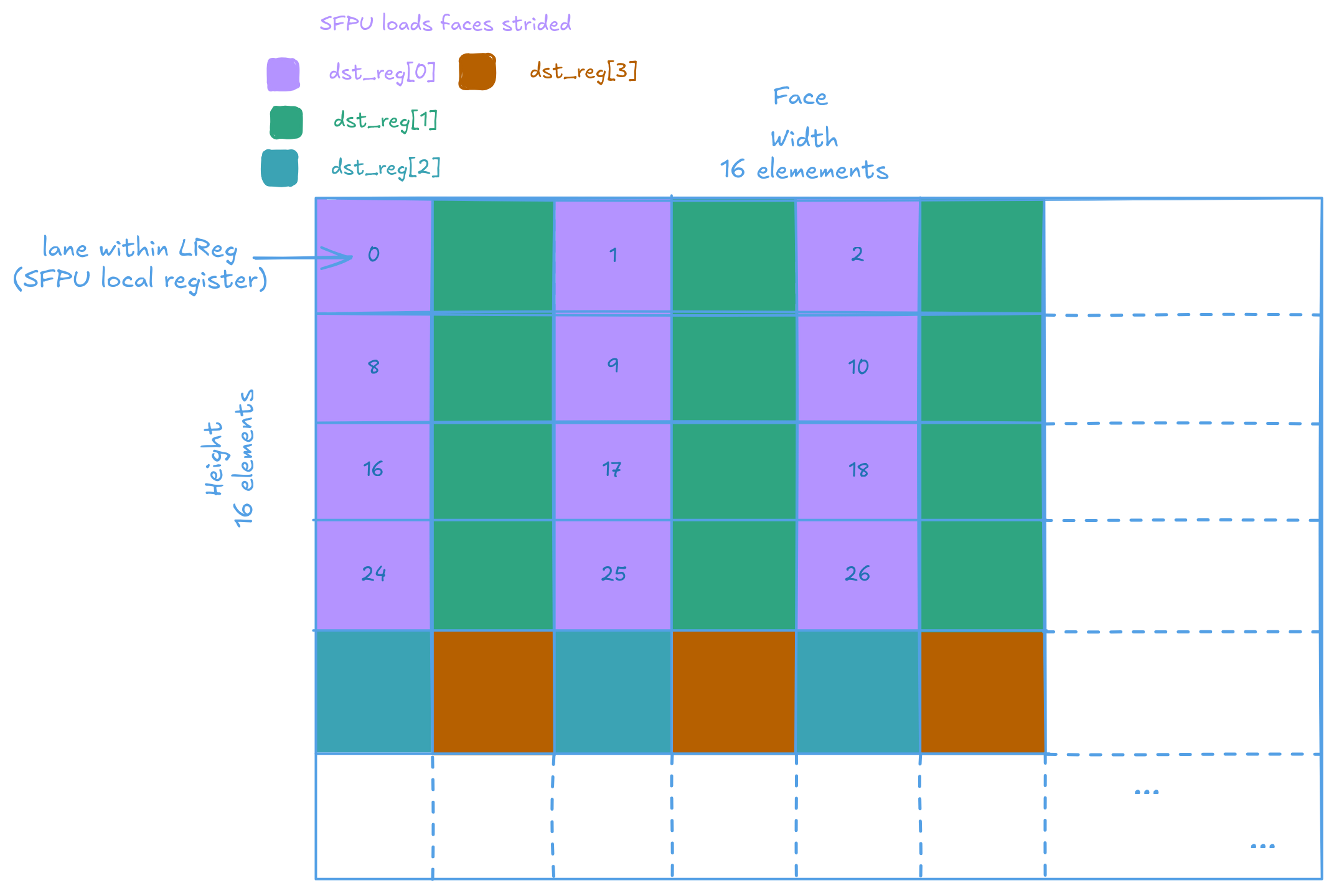
Therefor to calcualte the row index. We must take the vConstTileId variable (which contains [0, 2, 4... 30]). Mod it by 16. Add on the row offset of the face, then add 1 if we are processing the odd lanes.

The standard calculations to arrive the rotation angle used in RoPE is very inefficient on the SFPU. The SFPU is designed as a small but fast vector unit - it lacks a lot of complex function evaluation capabilities. No arbitrary pow(x, y), no division. Just basic arithmetic. There are some built in functions, but not designed as a part of the public interface.

The original formula freq = 1.0f / std::pow(10000.0f, exponent) has to be rewritten to avoid unsupported calculations:

• Replace power with exp: freq = 1.0f / exp(exponent * log(10000.0f))
• Convert the fraction into exponent: freq = exp(-exponent * log(10000.0f))
• Evaulate the log manually: freq = exp(-exponent * 9.21034037f)

The standard exp_tile API won't work here - they expect a full tile within Dst as the input. Instead we can find that that the public API internally calls ckernel::sfpu::_sfpu_exp2_21f_. Which does accept a SFPU variable as parameter. Likewise sin_tile is not directly usable for the same reason. However ckernel::sfpu::calculate_sine is very close to what we need. We can yank and modify it to suit our needs.

inline vFloat vector_sin(vFloat x)
{
    // handles input not in [-pi, pi]
    vFloat v = x * ckernel::sfpu::FRAC_1_PI;
    vInt whole_v = float_to_int16(v, 0);
    v -= int32_to_float(whole_v, 0);

    v = ckernel::sfpu::sfpu_sinpi<false>(v);
    v_if(whole_v & 1) { v = -v; }
    v_endif;
    return v;
}

inline void rope_face(int pos, int D_active, int vec_offset)
{
    float inv_d = 1.f/D_active;
    for (int i = 0; i < 8; i++) {
        // No mod operator on SFPI, use bit hack
        vFloat block_lane_id = int32_to_float((vConstTileId & 15) + vec_offset + i % 2);
        vFloat exponent = 2.f * block_lane_id * inv_d;

        vFloat term_to_exp = -exponent * 9.21034037f;
        vFloat freq = ckernel::sfpu::_sfpu_exp2_21f_<true>(term_to_exp);

        // Standard RoPE math
        vFloat angle = int32_to_float(pos) * freq;
        vFloat sin_value = vector_sin(angle);
        vFloat cos_value = vector_sin(ckernel::sfpu::PI_2 - angle);

        vFloat x = dst_reg[i];
        vFloat y = dst_reg[i+32];
        dst_reg[i] = x * cos_value - y * sin_value;
        dst_reg[i+32] = x * sin_value + y * cos_value;
    }
}

Numeric accuracy

The implementation works - for a while. However, numerical errors become significant when moving from pos = 1 to pos = 1000. The values deviate wildly, with some even being the negative of what they should be! What the actual.. it's just a rotation of the original value, so how could this happen? Since the algorithm works perfectly for lower positions and the logic remains unchanged regardless of the position values. Issue has to be something to do with numerical precision.

Much debugging later, I pinpointed freq as the culprit. The exponent matched the CPU's calculation exactly, bit for bit. However, multiplying by 10000 and then feeding that into sin() and cos() explained the issue: some values ended up as the negative of the reference, likely due to being half a phase off, causing the trigonometric outputs to invert. I dumped the variable into a CSV file, and the data confirmed my suspicion.

Some quick ROOT code to visualize what is going on (following code is slightly truncated to fit on a blog post. I choose ROOT as I don't want to deal with Pandas. Plus I love Minuit2's curve fitting and boundary handling capabilities; no need to worry about numerical edge cases).

// analysis.cpp
// Invoke with: root analysis.cpp
void analysis()
{
    auto* c1 = new TCanvas;
    c1->Divide(2, 2);
    c1->cd(1);

    auto df = ROOT::RDF::FromCSV("outputdata.csv");
    std::string col1 = "cpu_freq";
    std::string col2 = "device_freq";
    graph = df.Graph(col1, col2);
    graph->SetMarkerStyle(3);
    graph->Draw("ap");

    double error = 0.0;
    double max_error = 0.0;
    TH1D* h1 = new TH1D("h1", "Error Distribution;|CPU value - Device value|;Counts", 100, 0, max_error);
    df.Foreach([&](double cpu_angle, double device_angle) {
        double err = std::abs(cpu_angle - device_angle);
        error += err;
        if(err != 0)
            h1->Fill(err);
        max_error = std::max(max_error, err);
    }, {col1, col2});
    c1->cd(2);
    h1->Draw();

    auto err_df = df.Define("error", [&](double a, double b) {
        return std::abs(a - b);
    }, {col1, col2});
    graph_err = err_df.Graph(col1, "error");
    graph_err->SetMarkerStyle(3);
    c1->cd(3);
    graph_err->Draw("ap");

    func_err = std::make_shared<TF1>("func_err", "pol1", 0, 100);
    graph_err->Fit(func_err.get());
    func_err->SetLineColor(kRed);
    func_err->Draw("same");

    auto err_df2 = df.Define("error_normalized", [&](double a, double b) {
        return std::abs(a - b) / a;
    }, {col1, col2});
    graph_err2 = err_df2.Graph(col1, "error_normalized");
    graph_err2->SetMarkerStyle(3);
    c1->cd(4);
    graph_err2->Draw("ap");

    func_err2 = std::make_shared<TF1>("func_err2", "pol1", 0, 100);
    graph_err2->Fit(func_err2.get());
    gPad->SetLogx();
    func_err2->SetLineColor(kRed);
    func_err2->Draw("same");
}

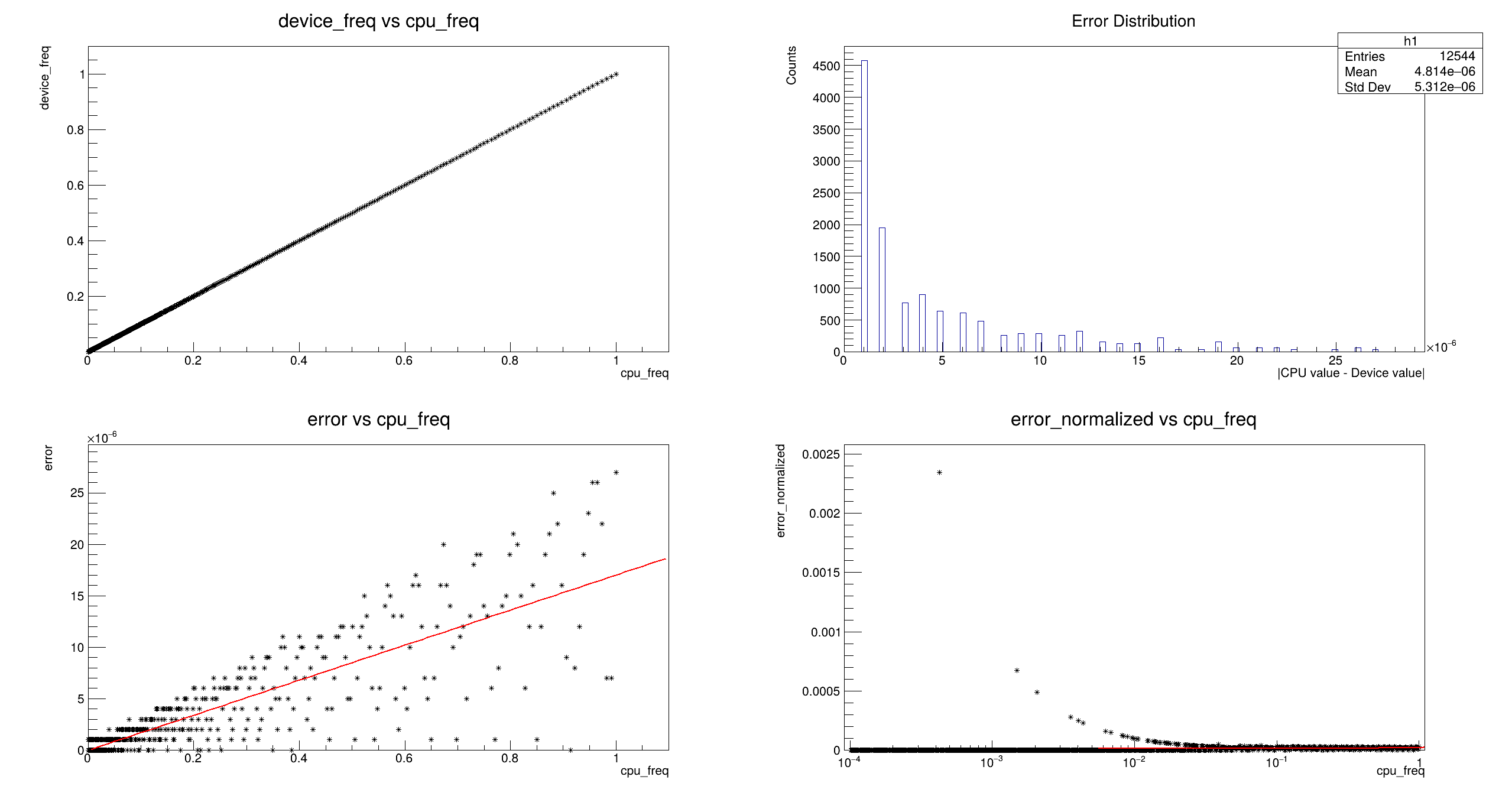
Running the above script yields the following plots. On the bottom left, titled error vs device_freq shows the absolute error between that the device calculated and what the CPU calculated - this error ought to be as low as possible. Now the problem makes sense. Given max error is ~0.0018, multiplying it by 10000 is 18. There is more then enough space for sine and cosines to be half a phase apart.

Looking into the paper of the exponential algorithm used by Metalium (I had to borrow someone's IEEE account), the exp_21f is one of the proposed algorithms to approximate the exponential function. It strikes a balance between speed and "good enough" accuracy. Apprantly it's not good enough for my use case. The exp_61f and exp_24f algorithms seem quite nice in the table. 50~100x accuracy should reduce the maximum error before going into trigonometry from 18 down to 0.18.

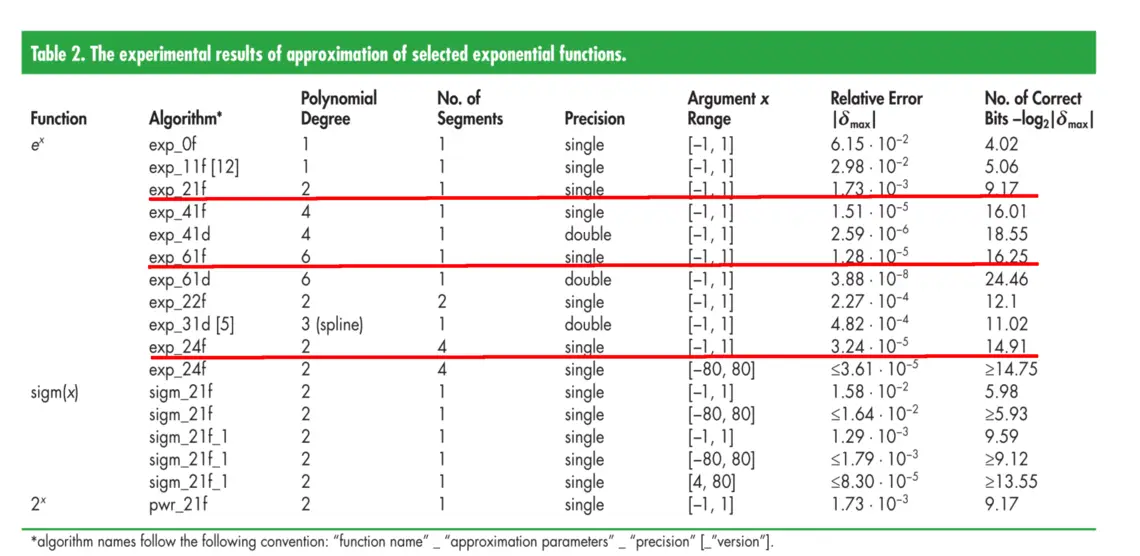
I ended up using exp_24f. I might have implemented it wrong, but, though exp_61f looks nice on paper. It does not behave well outside of the [-1, 1] range. While exp_24f behaves very well even from x=-10.

Fun fact. Somehow in the paper the author wrote:

float y,d1,d2,d3;
....
if(zif > 0x00200000)
{//second segment
    d1 = 0.37120473e-7f;
    d2 = 0x1113a74+zif;
    d3 = 0x9f16+zif;
}
else
{//first segment
    d1 = 0.31214472e-7f;
    d2 = 0x151d842+zif;
    d3 = 328.83582f+zif;
}

What? d3 is declared as a floating-point variable but is treated as an integer everywhere else (including the code Metalium uses, see the 21f algorithm in the same paper). The aim is to manipulate the mantissa, so it makes sense for d3 to be an integer. However, through trial and error, it turns out the author actually intended them to be floating-point values—i.e., d3 = 328.83582f. The above integer-like values all fit nicely into floating-point representation. The following is the core of the 24f algorithm in SFPU code (which treats d2 and d3 as integers—it works well enough and allows me to save on SFPU instructions).

v_if(zif > 0x00600000) {
    // Fourth segment (highest values of the mantissa)
    POLY_D1 = 0.52496276e-7f;
    POLY_D2 = 0x81354a;
    POLY_D3 = 0x10a440;it shh
}
v_elseif(zif > 0x00400000) {
    // Third segment
    POLY_D1 = 0.4414393e-7f;
    POLY_D2 = 0xcdf4b4;
    POLY_D3 = 0x3e4d6;
}
v_elseif(zif > 0x00200000) {
    // Second segment
    POLY_D1 =0.37120473e-7f;
    POLY_D2 = 0x1113a74;
    POLY_D3 = 0x9f16;
}
v_else {
    // First segment
    POLY_D1 = 0.31214472e-7f;
    POLY_D2 = 0x151d842;
    // Note: The original C code has a float constant here
    POLY_D3 = 328;
}
v_endif;

vFloat d1 = vFloat(POLY_D1);
vFloat d2 = int32_to_float(vInt(POLY_D2) + zif, 0);
vFloat d3 = int32_to_float(vInt(POLY_D3) + zif, 0);

Woohoo! exp_24f dramatically reduces the error compared to the builtin implementation. Max error is now somewhere in the 2x10^-5 range. And so much so that floating point blocky-ness can be seen in the plot itself (though this is printed via std::to_string, so it only prints effective digits). See the following diagram for a visual comparison:

Switching to exp_24f solves the accuracy issue singlehandily. Now pos=1000 have 100% pass rate. With maximum error of the final result at 0.03. Improvements can be made by using a better sin() approximation then what Metalium uses. But I consider what is achieved here good enough.

Profiling & Base Optimization

The code works. Now the question is—how slow is my implementation, and how fast can I make it? Fortunately, we have tools to help. Tenstorrent has forked the Tracy profiler, an excellent tool for GPU applications. To use it, the BUILD_TRACY CMake flag must be enabled in the host Metalium build. Since I am developing on a remote machine over SSH, I also need a local copy of Tracy running on my machine.

First, the Metalium build you are using has to have Tracy enabled. This can be achieved in 2 ways, either add the flag manually to the CMake command. Or add the --enable-tracy flag in the build script.

# If you are using CMake
cd /path/to/your/tt-metal/build
cmake . -DBUILD_TRACY=ON
ninja install

# If you are using the build script
cd /path/to/your/tt-metal
./build_metal.sh --enable-tracy

To create a capture. Start the cpature tool tt-metal/build/tools/profiler/bin/capture-release then your application. It should connect once the application starts and automatically saving the trace information.

The GUI needs to be built seperately (note that prior to this blog post, the GUI doesn't build on Linux properly, I have upstreamed a patch to make it work):

Reference build commands:

git clone https://github.com/Tenstorrent/tracy.git
cd tracy
cd profiler/build/unix
make -j8 release

It should result in a Tracy-release binary in the build folder. Run it. And an empty window should show up. The GUI can load and display the capture created earlier. Or connect to a running process and display the information on the fly.

IMPORTANT: The program being profiled acts as the server and capture tool a client. For remote development, create a forward tunnel to port 8086 on the remote machine. I use the following SSH command to establish the connection between the Tracy GUI and the program being profiled. Due to how SSH works, usually the Tracy GUI will wait for the server to come online. SSH will reject the connection if the application is not running at the time of connection. You must connect after starting the application.

I highly recommend adding the -C flag to since the datasteam from Tracy is very compressible.

ssh -C -NL 8086:localhost:8086 user@remote-machine

Or use a VPN that puts both machines under the same network. There's a million guides out there.

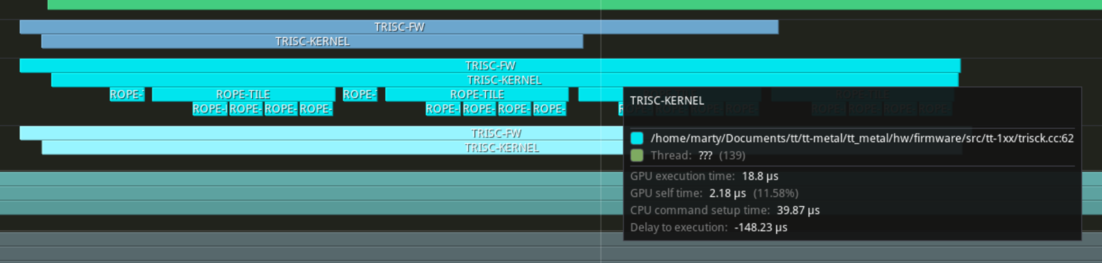
Now, in order to profile device kernels. We must set the TT_METAL_DEVICE_PROFILER environment flag; without the flag, kernel profiling will become null operation and no overhead will incur. And add a DeviceZoneScopedN object to the region of interest. The profile will record the time between object construction and destruction.

// in device kernel
inline void rope_tile(int pos, int D_active, int vec_offset)
{
    DeviceZoneScopedN("ROPE-TILE"); // insert this to create a profiling region

    // rest of the SFPI code
    math::set_dst_write_addr<DstTileLayout::Default, DstTileShape::Tile32x32>(0);
    math::set_addr_mod_base();
    ...
}

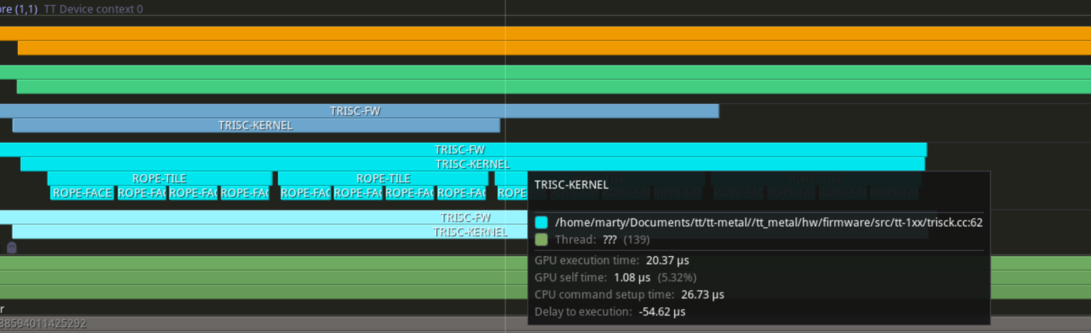
Ether connect to a running program or load up a captured trace. The window should now display the program running information.

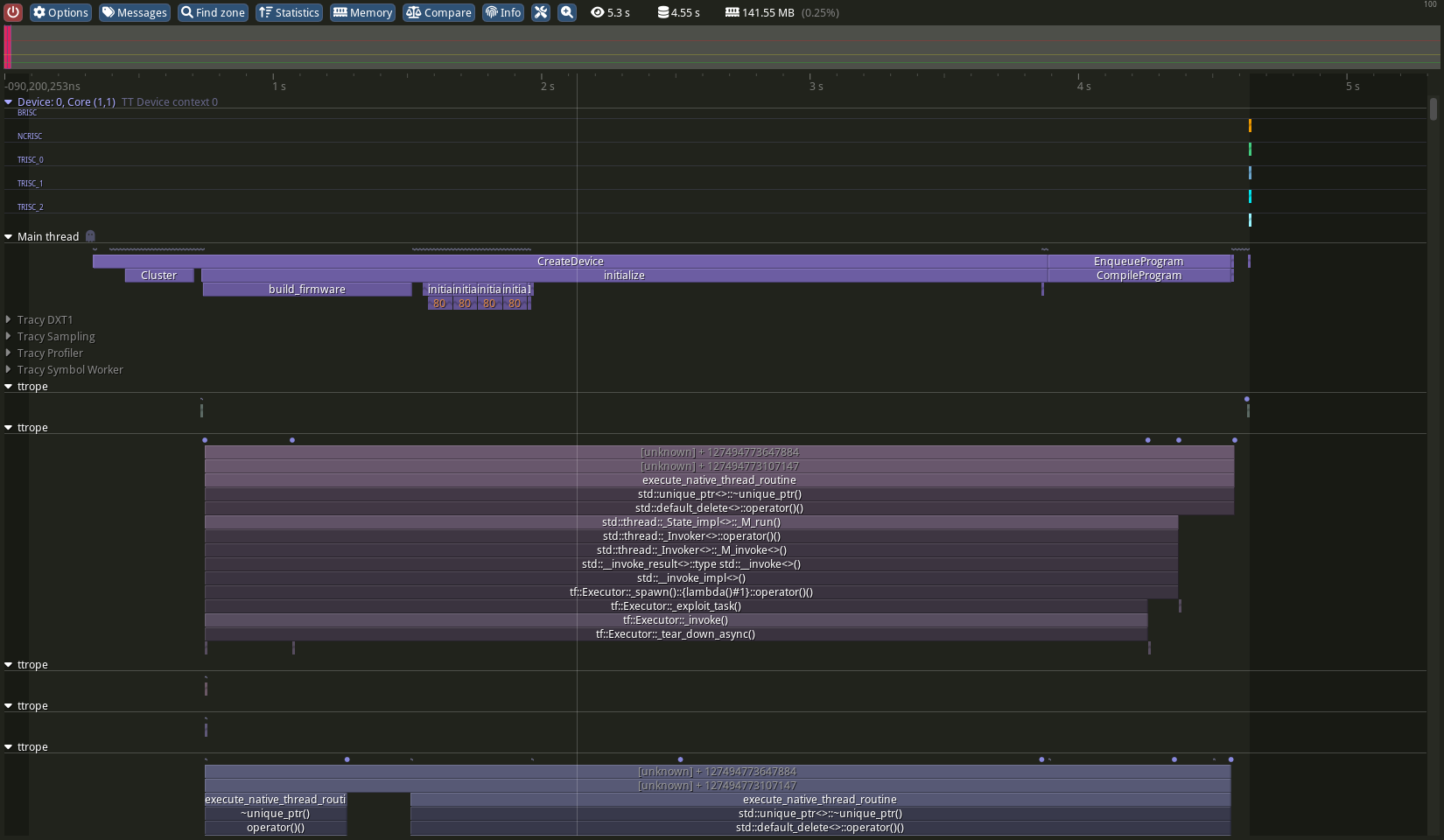
Zoom into the top left, where the kernel timing is. We can see the compute (to be precise, the SFPI code) takes 44us to process 4 pairs of tiles (or 11us per tile). That is SLOW, but not particularly unexpected. In rope_face, the line float inv_d = 1.f/D_active does floating point division, which the RISC-V cores on does not support and has to be done using softfp. Which is slow. And is currently doing 4 times per face.

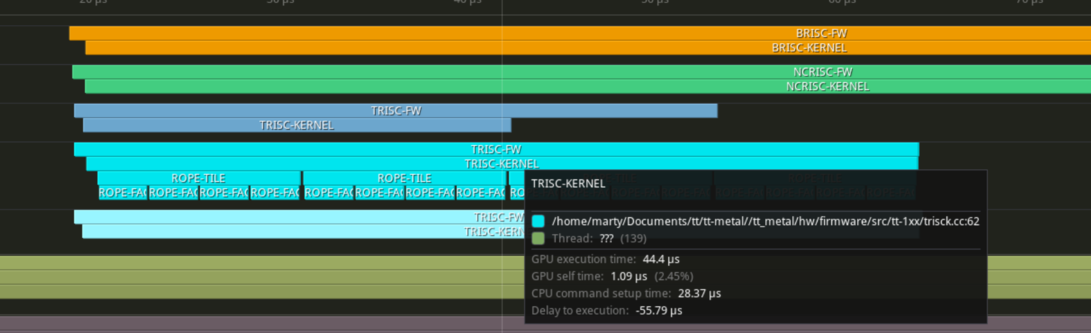
IMPORTANT: The overhead of profiling is nontrivial. You should not take microbenchmarking results and consider them the exact cycle count needed for the operation. That said, the delta in cycle count before and after code changes is still very useful.

Hoisting the floating point division

That division is the most obvious inefficiency and the easiest to address. Since parameters can be passed around like in any C program, and the D parameter is a single scalar (not a tensor), we can move the division to the beginning of the kernel. This allows the result to be shared across all pairs of tiles.

namespace NAMESPACE {
void MAIN {
    ...

    float inv_d = 1.f/(n_tiles_width_active * (32 / 2));

    ...
    for(...) {
        ...
        // during invocation
        MATH(rope_tile(1000, n_tiles_width_active * (32 / 2), j*32));
    }
    ...
    }
}

Re profiling shows the overall kernel execution time dropped from 5us from 44us to 39us. Pretty good for a simple optimization!

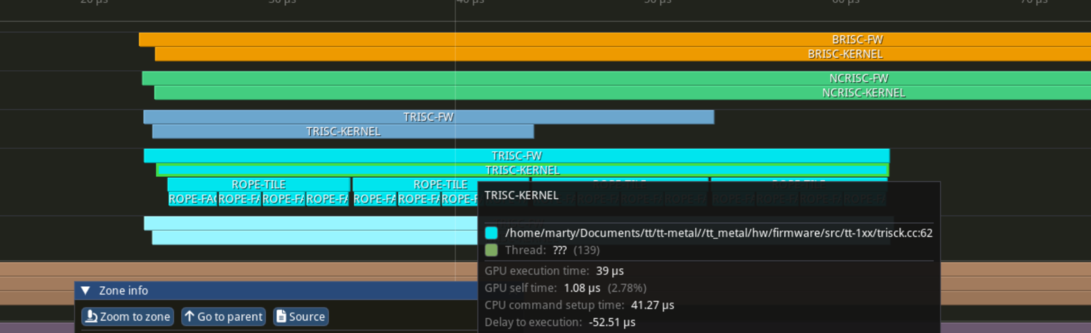
Reuse exponentiation

For accuracy, we implemented a custom exponential function. Our new implementation is much larger then the one that is used by default. It is bounded to be slow looking at the shear amount of code that forms it. Luckily, columns within the same tile (thus by extension each face) shares the same index in the input vector. We could reuse everything up to the point where we start to where each row diverges (keep in mind we still need to support different token index per row, as the GGML API asks)

for (int h = 0; h < 2; h++) {
    // No mod operator on SFPI, use bit hack
    vFloat block_lane_id = int32_to_float((vConstTileId & 15) + vec_offset + h);
    vFloat exponent = 2.f * block_lane_id * inv_d;

    vFloat term_to_exp = -exponent * 9.21034037f;
    vFloat freq = vector_exp(term_to_exp);
    for (int i = 0; i < 4; i++) {
        // Standard RoPE math
        vFloat angle = int32_to_float(pos) * freq;
        vFloat sin_value = vector_sin(angle);
        vFloat cos_value = vector_sin(ckernel::sfpu::PI_2 - angle);

        int idx = i*2+h;
        vFloat x = dst_reg[idx];
        vFloat y = dst_reg[idx+32];
        dst_reg[idx] = x * cos_value - y * sin_value;
        dst_reg[idx+32] = x * sin_value + y * cos_value;
    }
}

Wopping 17us reduced!

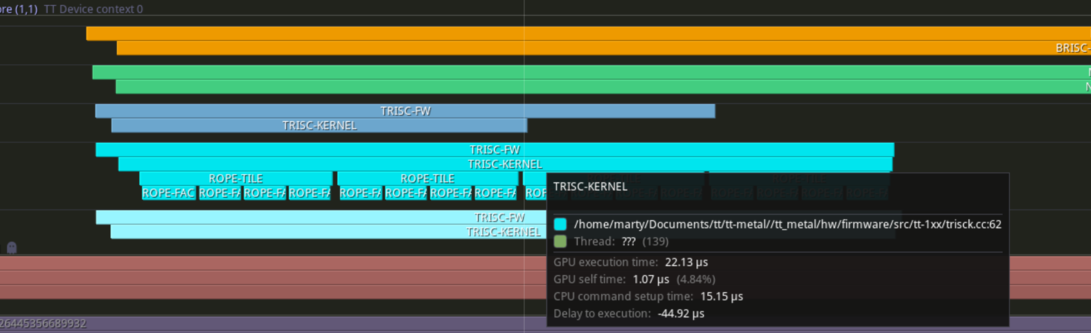
Numerical tricks

The next optimization we'll do is around the sine function, this is most likely just a few cycles of faster, but in HPC even one cycle is a lot. vector_sin always multiplies the input value with 1/pi in order to convert the expected range from [-pi, pi] to [-1, 1]. Then applying the antisymmetric property of sine to further reduce the range down to [0, 1] which the polynomial approximation uses. That's a load and multiplication we could avoid per invocation of the function. Let's turn vector_sin into vector_sin_phase - if we can amortize that multiplication away early on in the calculation:

inline vFloat vector_sin_phase(vFloat x)
{
    // was
    // vFloat v = x * ckernel::sfpu::FRAC_1_PI;
    vFloat v = x;
    vInt whole_v = float_to_int16(v, 0);
    v -= int32_to_float(whole_v, 0);

    v = ckernel::sfpu::sfpu_sinpi<false>(v);
    v_if(whole_v & 1) { v = -v; }
    v_endif;
    return v;
}

Reviewing the currnet logic of values going into the sine function, with the understanding that there's a implicit division by pi now:

// current logic
vFloat term_to_exp = -exponent * 9.21034037f;
vFloat freq = vector_exp(term_to_exp);

vFloat angle = int32_to_float(pos) * freq;
vFloat sin_value = vector_sin(angle);
vFloat cos_value = vector_sin(ckernel::sfpu::PI_2 - angle);

// What we need to turn it into
vFloat sin_value = vector_sin_phase(angle * ckernel::sfpu::FRAC_1_PI);
vFloat cos_value = vector_sin_phase((ckernel::sfpu::PI_2 - angle) * ckernel::sfpu::FRAC_1_PI);

We can find that the PI_2 term becomes 0.5. And we seem to multiply angle by 1/pi. Which by constantly moving it upwards and rewriting our equations:

• We need a new angle_phase = angle/pi
• Expanding that angle_phase = int32_to_float(pos) * freq / pi
• Evaluate the final two terms together freq/pi = vector_exp(term_to_exp) / pi
• And move the division into exponentiation freq/pi = vector_exp(term_to_exp - ln(pi))
• Finally expend the internal term to be exponented term_to_exp - ln(pi) = -exponent * 9.21034037f - ln(pi)
• As ln(pi) is a constant new_term_to_exp = -exponent * 9.21034037f - 1.14472988585f
• Also PI_2 / PI is 1/2 or 0.5

The core numerical calculations become

vFloat term_to_exp = -exponent * 9.21034037f - 1.14472988585f;
vFloat freq = vector_exp(term_to_exp);

vFloat angle = int32_to_float(pos) * freq;
vFloat sin_value = vector_sin_phase(angle);
vFloat cos_value = vector_sin_phase(0.5f - angle);

This optimization reduces execution time by another 1.13us

Using constant registers

Finally, Looking at the Low Level Kernels document from the official documentation site, several constants are defined and backed by hardware registers. In which vConst{Float,Int}Prgm[0-2] can be set to hold a single floating point or integer value at runtime (i.e. vConstFloatPrgm0 = 3.1415f or vConstIntPrgm1 = 1000).

Constant registers are implemented as objects which can be referenced wherever a vector can be used. On Wormhole and Blackhole the following variables are defined:
* vConst0
* vConst1
* vConst0p8373
* vConstNeg1
* vConstTileId, counts by two through the vector elements: [0, 2, 4..62]
* vConstFloatPrgm0, vConstIntPrgm0
* vConstFloatPrgm1, vConstIntPrgm1
* vConstFloatPrgm2, vConstIntPrgm2

That's use them then. We happen to have used several constants in the kernel. Removing the need to load them during kernel execution should make it slightly faster

inline void rope_tile_init(float inv_d)
{
    vConstFloatPrgm0 = 9.21034037f;
    vConstFloatPrgm1 = 1.14472988585f;
    vConstFloatPrgm2 = inv_d;
}

inline void rope_face(int pos, float inv_d, int vec_offset)
{
    ...

    for (int h = 0; h < 2; h++) {
        vFloat block_lane_id = int32_to_float((vConstTileId & 15) + vec_offset + h);
        vFloat exponent = 2.f * block_lane_id * vConstFloatPrgm2; // Use them like any other variables

        vFloat term_to_exp = -exponent * vConstFloatPrgm0 - vConstFloatPrgm1; // Use them like any other variables
        vFloat freq = vector_exp(term_to_exp);
        ...
    }
}

Another 0.5us faster!

Supporting per-row token position

2x faster is quite nice, and there's more tricks we can pull to maybe drop the execution down another 30%. However we have to stop here. We haven't fulfilled the GGML API yet. Currently we share the same token potion across the entire tile. However, GGML supports per-row position. The goal then, is eventually in tile_face, instead of loading a single integer as the token position, like we have been

NOTE: I made a blunder of universal scale here. Due to many factors (including me being stupid), I didn't notice GGML uses per-**batch** position. Which got me down the road of optimizing for per row data movement and loading. I only realized I made this mistake when I tried integrating with GGML.

vFloat angle = int32_to_float(pos) * freq;

To loading 4 integers into differnet rows within the vFloat variable.

vFloat vpos = int32_to_float(load_into_row(pos_ptr+offset));
vFloat angle = vpos * freq;

In order to do so, we must read position index from DRAM, store them in local SRAM in linear order. And pass that pointer to the compute cores. Which presents a problem - so far all operations we discussed works on a tile level, everything is a tile. But position indicies are not. They are raw vectors. What ever should we do..

TTNN supports row major layouts too. See how that's handled in the official document (you'll find the document very familare if you are a reader of this blog)

To store row major tensors, TTNN splits the tensor into rows and round robbin the rows across memory controllers. Like so:

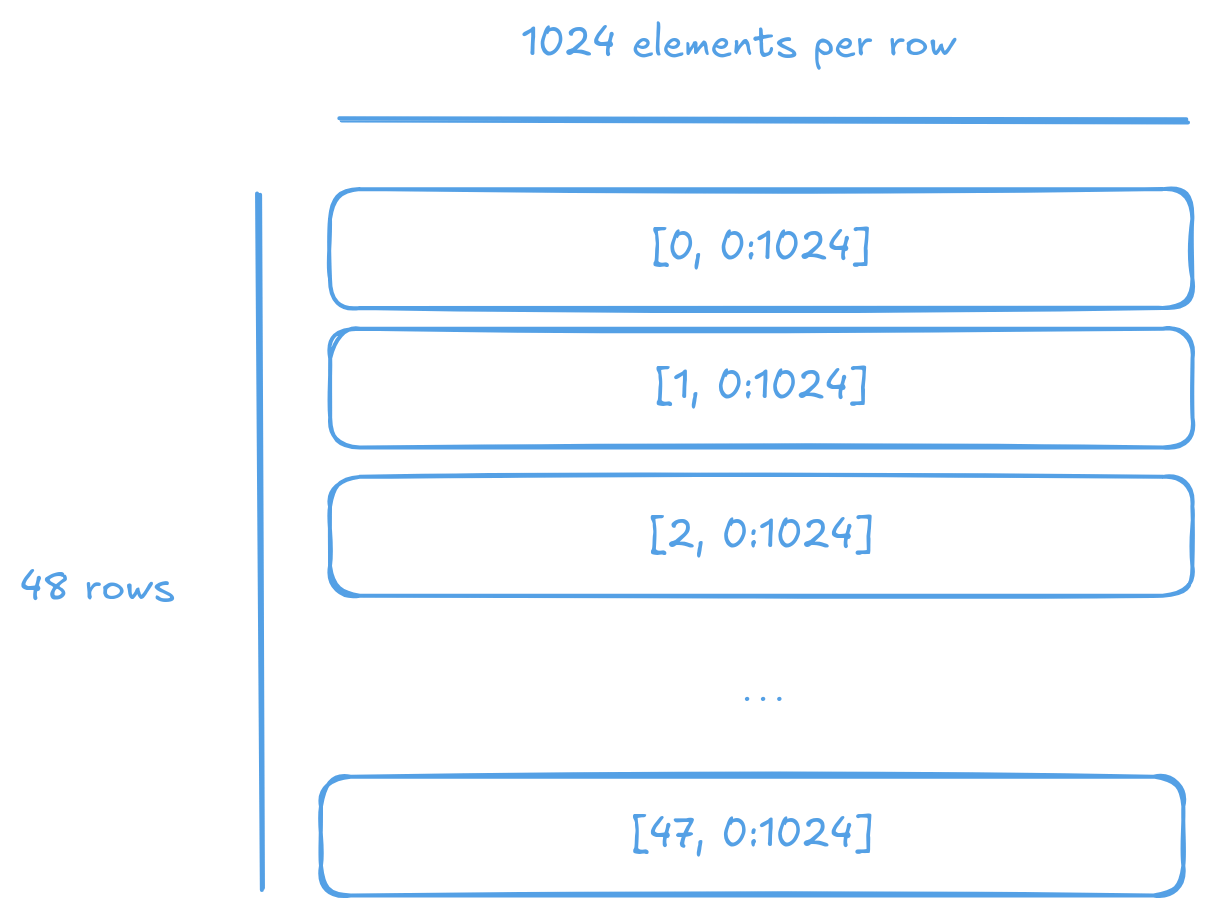
The standard noc_async_read_page API will happily read the rows into SRAM for us. But we ought to read 32 elements at a time. Just in case someone decided to send in a 50K word prompt and that turns into a 200KB buffer; let alone we need 2 of them to double buffer. And we only have 1.5MB of total SRAM per tensix core. Oh well, hacking time. Instead of raw reads.

We should manually calculate the addresses and read 128 bytes (32 four-byte int) at a time. On the host side, we create a buffer with the same scheme as TTNN would. And a circular buffer holding 32 integers at a time. Note that in this particular case, as there's only one row of indices, the page size and total size is the same for the index buffer - this will change when we support batching.

auto idxs = MakeBuffer(device,
    /*total_size=*/N*sizeof(int32_t),
    /*page_size=*/N*sizeof(int32_t),
    /*sram=*/false);

MakeCircularBuffer(program, core, tt::CBIndex::c_1,
    /*pagfe_size=*/ N*sizeof(int32_t),
    /*total_size=*/ 32*sizeof(int32_t),
    /*dtype=*/tt::DataFormat::Int32);

In the reader kernel, accessing subreagons of the index buffer goes through the same TensorAccessor object. But we manually set offset and read size when reading from DRAM.

constexpr auto idx_args = TensorAccessorArgs<src_args.next_compile_time_args_offset()>();
// Cannot rely of get_tile_size() since we are not reading a tile at a time. Manual
// calculation of page size (or just pass in as kernel parameter).
uint32_t idx_page_size = n_tiles_height*32*sizeof(int32_t);
const auto idx = TensorAccessor(idx_args, idx_addr, idx_page_size);
constexpr uint32_t cb_in1 = tt::CBIndex::c_1; // where we will be pushing index data

for(uint32_t h = 0; h < n_tiles_height; h++) {

    cb_reserve_back(cb_in1, 1);
    uint32_t cb_idx_addr = get_write_ptr(cb_in1);
    // Recall we only have one row of indices now. So always on page 0
    //                                    v
    uint64_t read_addr = idx.get_noc_addr(0, /*offset=*/32*sizeof(int)*h);
    // Read 32 integers at a time
    noc_async_read(read_addr, cb_idx_addr, 32*sizeof(int));
    noc_async_read_barrier();
    cb_push_back(cb_in1, 1);

    ...
    // Rest of the reader kernel
}

Now, in the compute kernel. We don't use get_read_ptr to access the SRAM address. Instead use cb_get_tile - this API also handles CB synchronization between the 3 compute cores.

for(uint32_t i = 0; i < n_tiles_height; i++) {
    // Read the address of the CB pushed by the reader kernel
    cb_wait_front(cb_in1, 1);
    int* idxs = nullptr;
    cb_get_tile(cb_in1, 0, &idxs);
    // IDK why, but documented to need shift of 16 bytes
    idxs += 4;

    // Rest of the compute loop for RoPE
    ...
    for(uint32_t j = 0; j < n_tiles_width_active/2; j++) {
        ...
        // Pass the indices pointer to the SFPI function
        MATH(rope_tile(idxs, inv_d, j*32));
        ...
    }

    cb_pop_front(cb_in1, 1);
}

Pass it down the chain of compute calls and applying the correct offset so each face has the right pointer.

inline void rope_tile(int* pos, float inv_d, int vec_offset)
{
    ...
    for (int face = 0; face < 4; face++) {
        // Where are we along the vector
        int internal_offset = ((face % 2 == 0) ? 0 : 16);
        // Which index we should read from
        int idx_offset = face > 1 ? 16 : 0;
        rope_face(pos + idx_offset, inv_d, vec_offset + rope_tile_precompute_pos(idxs)internal_offset);
        TTI_SETRWC(p_setrwc::CLR_NONE, p_setrwc::CR_D, 8, 0, 0, p_setrwc::SET_D);
        TTI_SETRWC(p_setrwc::CLR_NONE, p_setrwc::CR_D, 8, 0, 0, p_setrwc::SET_D);
    }
    ...
}

Now each face has a int* pointer pointing to the position values in SRAM. The custom load_into_row function takes in a pointer and load the first 4 values and returns a vInt. Again bit tricks here. As there is not division operation available. We mask away the lower 4 bits and check the remaining bits to determine which row to load.

inline vInt load_into_row(int* ptr)
{
    // Recall vConstTileId:
    //    contains [0, 2, 4, 6, 8, 10, 12, 14, 16, 18 ... 62]
    // By anding it with ~15 (bit inverse of 15) we mask away the lower 3 bits. Thus
    //    remains [0, 0, 0, 0, 0, 0, 0, 0, 16, 16, ... 48]
    // Which we can then check the remaining bits to determine which row to load.
    vInt row_mask = vConstTileId & (~15);
    vInt v = ptr[0]; // Unconditional load (avoid one comparsion)
    v_if(row_mask == 16) { // Load from the next row
        v = ptr[1];
    }
    v_elseif(row_mask == 32) { // Load from row 2
        v = ptr[2];
    }
    v_elseif(row_mask == 48) { // Load from row 3
        v = ptr[3];
    }
    v_endif;
    return v;
}

inline void rope_face(int* pos, float inv_d, int vec_offset)
{
    ...
    for(...) {
        vFloat vpos = int32_to_float(load_into_row(pos+i*4));
        vFloat angle_phase = vpos * freq;
        ...
    }
}

It's a long path to getting independent indices. Unfortunately now we are back to 32us to process 4 pairs of tiles. Yikes.

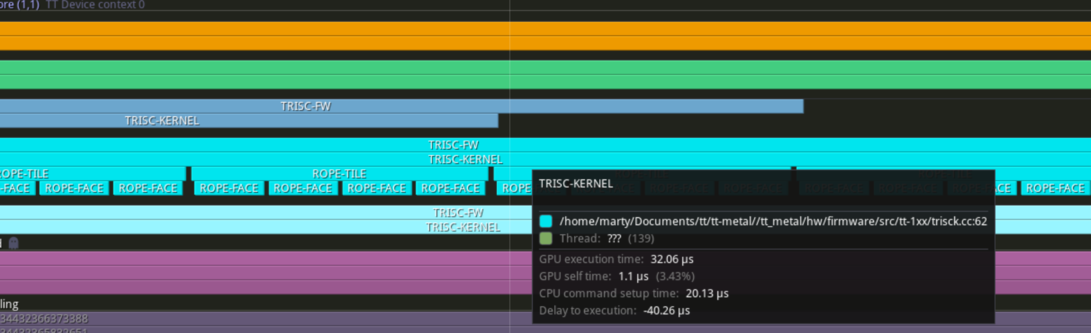
Optimization: Abusing Dst as data storage

It needs some optimization. I asked around and even looked at the ISA documentation. I couldn't come up with a better solution than what I implemented to load integers into rows. Fine, I'll have to amortize the cost of the loads. Currently, the token positions are loaded for each pair of vectors to perform RoPE, which doesn't make much sense since the entire face shares the same set of 16 positions. Furthermore, the entire row of tiles shares the same 32 token positions. If only there were a way to persist vector values across multiple iterations (NOTE: SFPI does not support spilling to SRAM, and SFPU can only communicate with SRAM using the packer).

There is one place that we could store data into - the Dst registers. However some very important caveats

• Position indices can reach values in the millions, necessitating the use of FP32 in Dst (as neither bfloat16 nor int16 can represent values in this range). This requires setting fp32_dest_acc_en to true in the compute kernel configuration.
• For performance reasons, each time tile_regs_acquire is called, only half of the actual Dst register is made available. This means we need to generate the position indices twice.
• Our kernel currently auto-increments dst_reg using TTI_SETRWC. This behavior needs to be disabled.

That's do that. First, the function to generate and store the position values for us. Since currently we are using tile 0 and 1 for data input/output. The stored position indices will be stored in tile 2. And since each tile is 32 LReg wide, tile 2 starts at offset 64.

inline void rope_tile_precompute_pos(int* pos)
{
    DeviceZoneScopedN("ROPE-TILE-PRECOMP-POS");
    math::set_dst_write_addr<DstTileLayout::Default, DstTileShape::Tile32x32>(0);
    math::set_addr_mod_base();
    TTI_STALLWAIT(p_stall::STALL_SFPU, p_stall::MATH);

    for (int i=0;i<8;i++) {
        vFloat vpos = int32_to_float(load_into_row(pos+i*4));
        dst_reg[64+i] = vpos;
    }

    math::clear_dst_reg_addr();
    TTI_STALLWAIT(p_stall::STALL_CFG, p_stall::WAIT_SFPU);
    math::clear_addr_mod_base();
}

Next, we had to disable auto dst_reg increment that is meant to help operator writers to keep in sync with where each face is - now, invoking rope_face looks like this.

for (int face = 0; face < 4; face++) {
    int internal_offset = ((face % 2 == 0) ? 0 : 16);
    int idx_offset = face > 1 ? 16 : 0;
    // Now we had to tell rope_face which face it is processing now
    //                                                               vvvv
    rope_face(pos + idx_offset, inv_d, vec_offset + internal_offset, face);
    // These are deleted
    // TTI_SETRWC(p_setrwc::CLR_NONE, p_setrwc::CR_D, 8, 0, 0, p_setrwc::SET_D);
    // TTI_SETRWC(p_setrwc::CLR_NONE, p_setrwc::CR_D, 8, 0, 0, p_setrwc::SET_D);
}

And in rope_face two things has to happen - manual offset when accessing dst_reg and instead of loading from integers. We direcly load from Dst.

int face_row = face_idx / 2; // If we are in the 1st row of face, helps determine which position to load
int dst_offset = face_idx*8; // Auto dst_reg increment is diabled. Calculate the offset of the current face
for (int h = 0; h < 2; h++) {
    vFloat block_lane_id = int32_to_float((vConstTileId & 15) + (vec_offset + h));
    vFloat exponent = block_lane_id * vConstFloatPrgm2;

    vFloat term_to_exp = -exponent * vConstFloatPrgm0 - vConstFloatPrgm1;
    vFloat freq = vector_exp(term_to_exp);
    for (int i = 0; i < 4; i++) {
        vFloat vpos = dst_reg[64+face_row*4+i]; // Load the precompued position values

        // Same RoPE as before
        vFloat angle_phase = vpos * freq;
        vFloat sin_value = vector_sin_phase(angle_phase);
        vFloat cos_value = vector_sin_phase(0.5f - angle_phase);

        size_t idx = i*2+h;
        // Auto dst_reg increment is diabled. `dst_offset` is added to manually
        // calculate where to read and write
        vFloat x = dst_reg[dst_offset+idx];
        vFloat y = dst_reg[dst_offset+idx+32];
        dst_reg[dst_offset+idx] = x * cos_value - y * sin_value;
        dst_reg[dst_offset+idx+32] = x * sin_value + y * cos_value;
    }
}

Finally the precomputation has to be invoked for the first 2 iterations of a row in the main kernel - to populate (the double buffered) Dst with the precomputed position values.

for(uint32_t j = 0; j < n_tiles_width_active/2; j++) {
    cb_wait_front(cb_in0, 2);
    tile_regs_acquire();
    if(j<2) {
        MATH(rope_tile_precompute_pos(idxs));
    }

    ...
    // Rest is the same
}

Pew... That's a lot of small changes. And we are back down to 22.6us

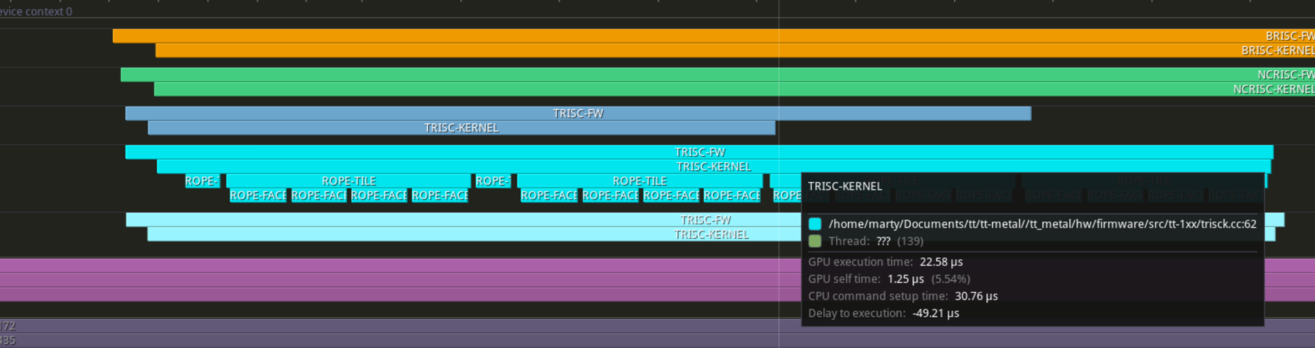
Reusing exponent within a tile

In the same spirit of reusing token positions, the exponent is also consistent within the same column of a face within a tile. We have already used this fact within a face to reduce the number of exponential operations. By extending this optimization across faces, we can further enhance performance.

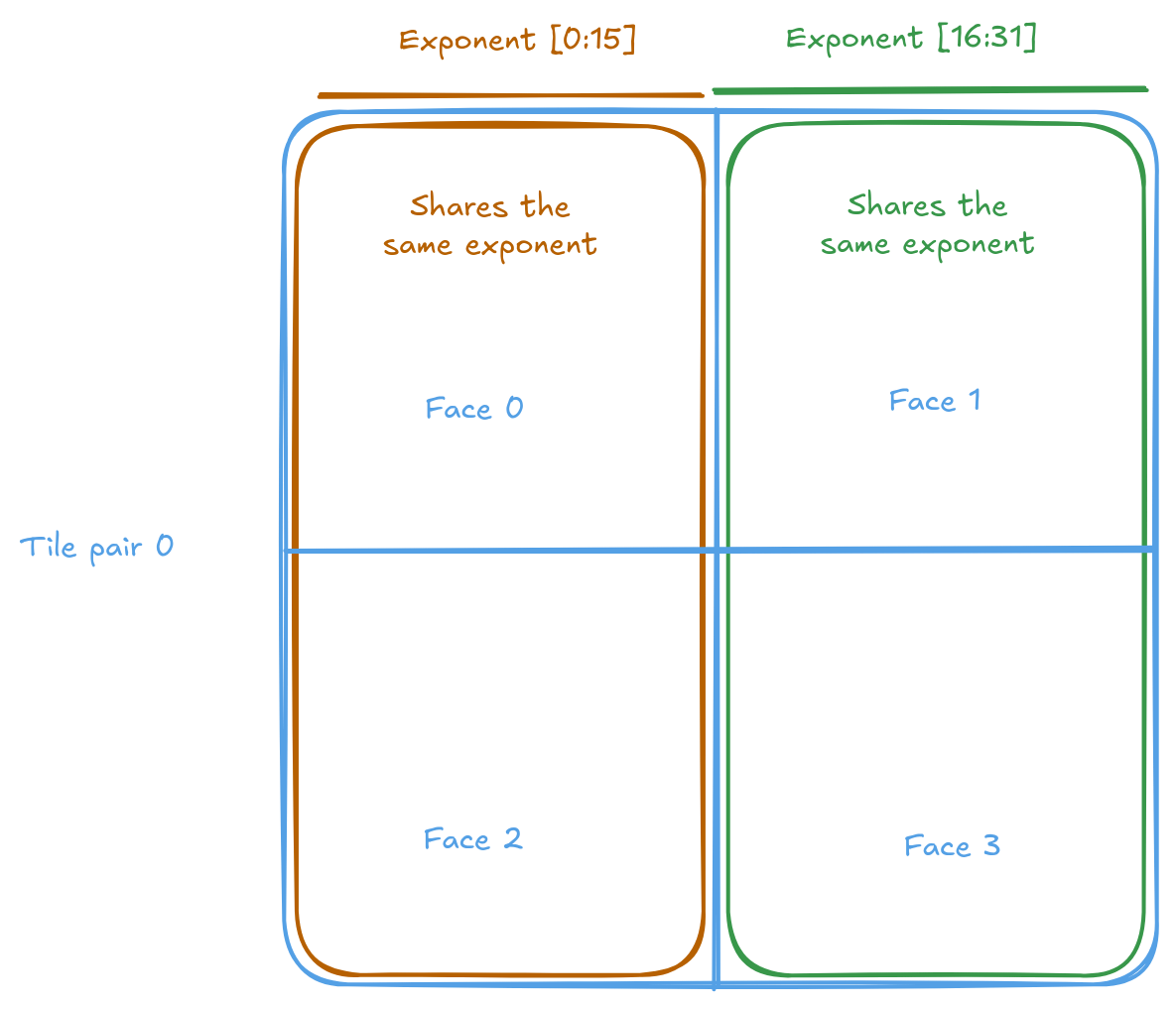
NOTE: Similar to reusing token positions across tiles, it is possible to reuse the exponents across tiles as well. However, reusing exponents potentially requires significantly more space than reusing token positions. Each tile needs 4 vectors of exponents. Since there are only 2 free tiles (or 64 free vectors) in Dst and we already use 8 vectors to hold positions, this leaves 64 - 8 = 56 vectors available for exponents. This allows for at most 896 active dimensions to apply RoPE to. This is sufficient for LLMs; for example, Gemma 2 2B uses 128 active dimensions. While it is possible to work around this limitation with additional logic. In the name of not loosing generality - I will avoid reusing exponents across tiles.

Prior to invoking the actual RoPE computation. Generate the exponents and store them in Dst. Since we used the first 8 vectors to hold the token position. Exponents is stored from the 8th vector.

// Generate the exponents for the current tile and store them in Dst
for(int i=0;i<4;i++) {
    int internal_offset = ((i / 2 == 0) ? 0 : 16);
    int pos_in_vector = vec_offset + internal_offset;
    vFloat block_lane_id = int32_to_float((vConstTileId & 15) + (pos_in_vector + i % 2));
    vFloat exponent = block_lane_id * vConstFloatPrgm2;

    vFloat term_to_exp = -exponent * vConstFloatPrgm0 - vConstFloatPrgm1;
    vFloat freq = vector_exp(term_to_exp);
    dst_reg[64+8+i] = freq;
}

// The same rope_face invocation
for (int face = 0; face < 4; face++) {
    int internal_offset = ((face % 2 == 0) ? 0 : 16);
    int idx_offset = face > 1 ? 16 : 0;
    rope_face(pos + idx_offset, inv_d, vec_offset + internal_offset, face);
}

And just load the exponents from Dst in the compute loop.

for (int h = 0; h < 2; h++) {
    vFloat freq = dst_reg[64+8+face_col*2+h];
    ...
    // Rest of RoPE
}

Support for batching

Batching support is straightforward compared to the complexities discussed earlier in this article. The process involves adding an extra parameter and an outer loop. On the host side, a new parameter B is introduced to represent the batch size. The main adjustment required is changing the shape of the index tensor to [B, N]. Since row-major tensors on TTNN store an entire row as a single page, the total size of the tensor is updated, while the page size remains unchanged.

constexpr size_t B = 4; // New parameter
constexpr size_t D = 2048;
constexpr size_t D_active = 256;
constexpr size_t N = 32;

...

auto src = MakeBuffer<float>(device, B * Dt * Nt);
auto dst = MakeBuffer<float>(device, B * Dt * Nt);

// Since the shape of the index tensor is [B, N] and as per how row major tensors
// work on TTNN (each row is a single page). The total size of the index buffer
// is B*N*sizeof(int32_t) while page size remains N*sizeof(int32_t)
auto idxs = MakeBuffer(device, B*N*sizeof(int32_t), N*sizeof(int32_t), false);

Device side, recall that in the reader kernel we used to only read from page 0. Now the page follows the batch index.

uint32_t batch_size = get_arg_val<uint32_t>(5); // new parameter
for(uint32_t b = 0; b < batch_size; b++) { // new loop introduced
    for(uint32_t h = 0; h < n_tiles_height; h++) {
        cb_reserve_back(cb_in1, 1);
        uint32_t cb_idx_addr = get_write_ptr(cb_in1);
        uint64_t read_addr = idx.get_noc_addr(b, 32*sizeof(int)*h); // Reading from page B
        noc_async_read(read_addr, cb_idx_addr, 32*sizeof(int));
        noc_async_read_barrier();
        cb_push_back(cb_in1, 1);
        ...
    }
}

Parallelizing

So far, the RoPE implementation runs on a single Tensix core. However, there are 56 of them on a single N300 chip and 120 on a single p150 - using only 1/120th of the available compute is inefficient. The challenge being the workload's two distinct phases: processing tiles that require RoPE (compute-bound) and simply copying passive tiles (memory-bound). Treating both phases as if they require the same resources would be inefficient, as the two phases are constrained by different bottlenecks. Naively parallelizing both phases together would combine the worst characteristics of each. On the other hand, scheduling work by rows can avoid this issue, but in practice, there may not be enough rows to fully utilize all cores, leading to underutilization.

So, we schedule both the active and passive phase separately. Then combine the schedule to run on a single kernel. See the following diagram for an illustration of the approach.

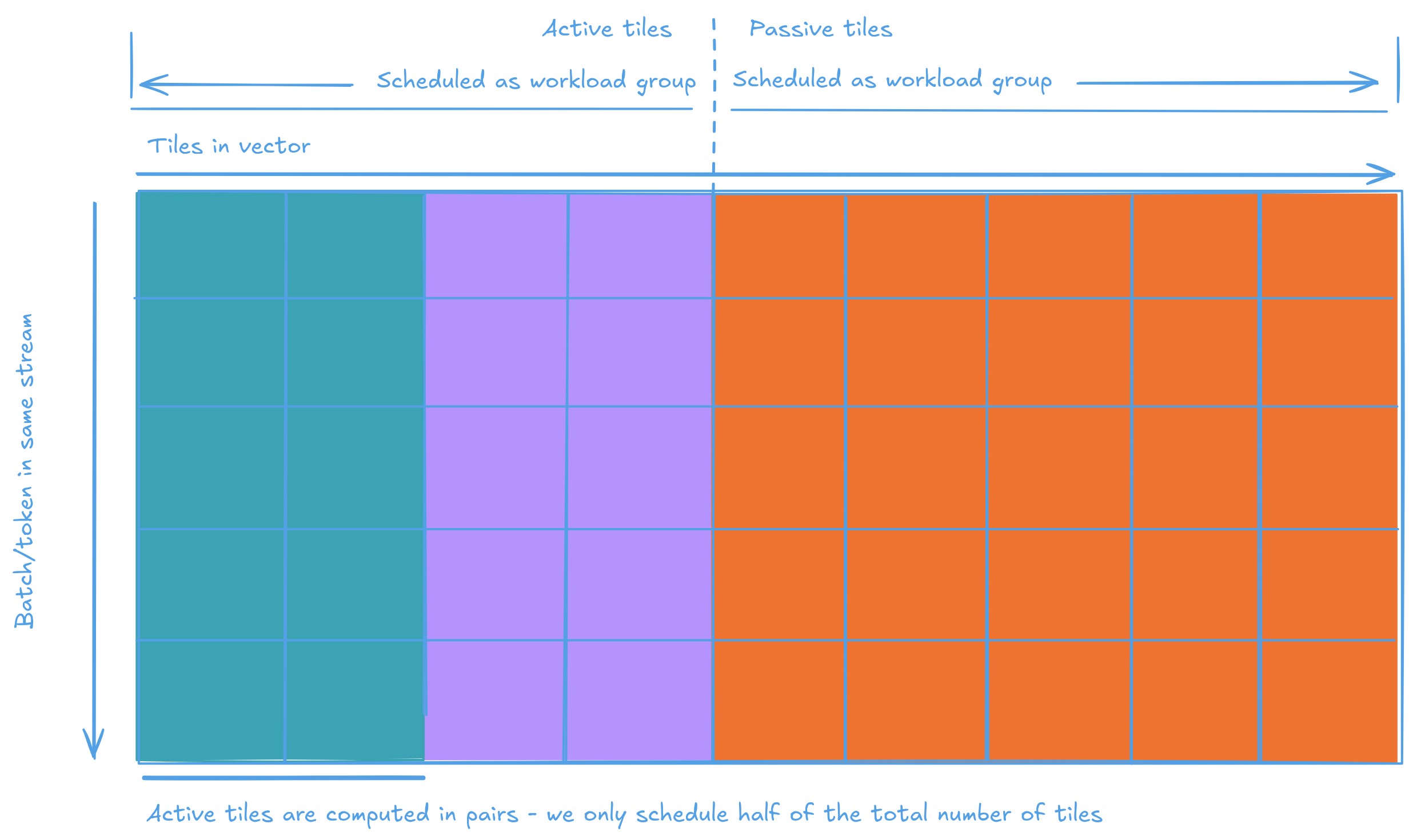
Flattening the nested loops

The first problem to address is that we currently use three nested loops to iterate over the dimensions. Since Metalium does not provide task scheduling utilities like OpenCL's get_global_id() or CUDA's threadIdx, the responsibility of dividing the workload into smaller subsets and assigning them to different cores falls on the programmer. Task scheduling itself is a separate challenge that we can tackle later. For now, the core loops need to be flattened into a single loop, with the b, h, and w indices calculated within the loop body. This approach will introduce some overhead, but it is necessary to enable parallelization. To simplify debugging, we can initially execute the entire computation (and data movement) on a single core.

We introduce new variables in the kernels - active_begin, active_end, passive_begin and passive_end denoting which tile in core needs to be processed by the active and passive phases respectively. For execution on a single core, we can simply set active_begin to 0, active_end to the total number of active tiles divided by two (as they are pairs), passive_begin to 0, and passive_end to the total number of passive tiles.

uint32_t active_begin = get_arg_val<uint32_t>(6); // or whatever index in that kernel should be
uint32_t active_end = get_arg_val<uint32_t>(7);
uint32_t passive_begin = get_arg_val<uint32_t>(8);
uint32_t passive_end = get_arg_val<uint32_t>(9);

On the host side, the kernel parameters are set accordingly

uint32_t active_tiles = B*Nt*(D_activet/2);
uint32_t passive_tiles = B*Nt*(Dt - D_activet);
SetRuntimeArgs(program, reader, core, std::vector<uint32_t>{..., 0, active_tiles, 0, passive_tiles});
// recall compute the kernel doesn't care about passive tiles
SetRuntimeArgs(program, compute, core, std::vector<uint32_t>{...,0 , active_tiles});
SetRuntimeArgs(program, writer, core, std::vector<uint32_t>{..., 0, active_tiles, 0, passive_tiles});

The writer kernel is the most straightforward of the three to understand, though it still involves some complexity due to the presence of two sets of workload indices: active and passive tile indices. To simplify matters, we take advantage of the fact that, in RoPE, there is no interaction between rows within a tensor. This allows us to effectively fold the batch dimension into the height dimension. The code then infers the dimensions and strides of the active and passive tiles based on the input matrix dimensions and the size of the active region - height doesn't mean hight in the kernel. Yay (sad donky face).

for(uint32_t active_id=active_begin; active_id<active_end; active_id++) {
    // Convert the active tile index to a 2D coordinate
    // NOTE: Height is not really height here. There's no interaction between rows within a tensor in RoPE
    //  the batch dimension is folded into the height dimension
    uint32_t h = active_id / (n_tiles_width_active/2);
    uint32_t w = active_id % (n_tiles_width_active/2);

    // Same logic as before to calculate the tile indices residing in DRAM and write back
    cb_wait_front(cb_out0, 2);
    uint32_t tile_idx = h * n_tiles_width + w;
    uint32_t tile_idx2 = h * n_tiles_width + w + n_tiles_width_active/2;
    uint32_t cb_out_addr = get_read_ptr(cb_out0);
    noc_async_write_tile(tile_idx, dst, cb_out_addr);
    noc_async_write_tile(tile_idx2, dst, cb_out_addr + tile_size_bytes);
    noc_async_write_barrier();
    cb_pop_front(cb_out0, 2);
}

// Same story for passive tiles
// * Calculate the 2D coordinate of the tensor (with batch folded in)
// * Convert to index in DRAM
// * Write to DRAM
uint32_t n_tiles_width_passive = n_tiles_width - n_tiles_width_active;
for(uint32_t passive_id = passive_begin; passive_id < passive_end; passive_id++) {
    uint32_t h = passive_id / n_tiles_width_passive;
    uint32_t w = passive_id % n_tiles_width_passive + n_tiles_width_active;

    cb_wait_front(cb_bypass, 1);
    uint32_t cb_bypass_addr = get_read_ptr(cb_bypass);
    uint32_t tile_idx = h * n_tiles_width + w;
    noc_async_write_tile(tile_idx, dst, cb_bypass_addr);
    noc_async_write_barrier();
    cb_pop_front(cb_bypass, 1);
}

The compute kernel has two extra complexities the deal with - it accepts the token position from the reader kernel through a circular buffer and it needs the position cache established on both half of the Dst registers. Not worries. Nothing a little state machine can't handle

// A little bit of state to track where the position CB and if we need to populate the Dst with position cache
uint32_t last_h = (uint32_t)-1;
bool need_pop = false;
int cached_populated = 0;

int* idxs = nullptr;
for(uint32_t active_id=active_begin; active_id<active_end; active_id++) {
    // Same trick, convert the active_id to a tile corrdinate
    uint32_t h = active_id / (n_tiles_width_active/2);
    uint32_t w = active_id % (n_tiles_width_active/2);
    cb_wait_front(cb_in0, 2);
    tile_regs_acquire();

    // If we are on a new row - wait for the position indices to be sent over
    if(last_h != h) {
        if(need_pop) {
            // Remember to remove the one from the last row!
            cb_pop_front(cb_in1, 1);
        }
        cb_wait_front(cb_in1, 1);
        need_pop = true;
        cb_get_tile(cb_in1, 0, &idxs);
        idxs += 4;
        last_h = h;
        // Setup state so we can track if Dst is populated
        cached_populated = 0;
    }

    // If we need to setup position cache in Dst
    if(cached_populated < 2) {
        // Setup the position cache and increment the counter
        MATH(rope_tile_precompute_pos(idxs));
        cached_populated++;
    }
    // Same logic as the previous compute kernel to invoke and generate the RoPE results
    copy_tile_init(cb_in0);
    copy_tile(cb_in0, 0, 0);
    copy_tile(cb_in0, 1, 1);
    MATH(rope_tile(idxs, inv_d, w*32));
    tile_regs_commit();
    tile_regs_wait();

    cb_reserve_back(cb_out0, 2);
    pack_reconfig_data_format(cb_out0);
    pack_tile(0, cb_out0, 0);
    pack_tile(1, cb_out0, 1);
    tile_regs_release();
    cb_push_back(cb_out0, 2);
    cb_pop_front(cb_in0, 2);
}

// If we have consumed from the position CB. Remember to pop it
if(need_pop) {
    cb_pop_front(cb_in1, 1);
}

The reader kernel has an additional pain to deal with. Like the compute kernel is cares about the iteration is - it needs to read the position indices from DRAM if it just switched to reading a new row of tiles. But beyond that, it uniquely cares about the batch it is on. RoPE itself doesn't care. But the index stored in row major format does. Remember that the index tensor have shape [batch, n_vectors]

// Track when we need to read new positions
uint32_t last_h = (uint32_t)-1;
for(uint32_t active_id=active_begin; active_id<active_end; active_id++) {
    uint32_t h = active_id / (n_tiles_width_active/2);
    uint32_t w = active_id % (n_tiles_width_active/2);

    // Read position when first entering a new row
    if(last_h != h) {
        // The position tensor has shape [batch, n_vectors]. We need do calculate the batch
        // number of the current row and read from the correct location
        uint32_t b = h / n_tiles_height;

        // Idential logic as before
        cb_reserve_back(cb_in1, 1);
        uint32_t cb_idx_addr = get_write_ptr(cb_in1);
        // one small different - now batch is folded into h, need to remove it to get the real h
        //                                                       vvvvvvvvvvvvvvvvv
        uint64_t read_addr = idx.get_noc_addr(b, 32*sizeof(int)*(h%n_tiles_height));
        noc_async_read(read_addr, cb_idx_addr, 32*sizeof(int));
        noc_async_read_barrier();
        cb_push_back(cb_in1, 1);
        last_h = h;
    }

    // Same logic as before reading active tiles
    cb_reserve_back(cb_in0, 2);
    uint32_t cb_src_addr = get_write_ptr(cb_in0);
    uint32_t tile_idx =  h * n_tiles_width + w;
    noc_async_read_tile(tile_idx, src, cb_src_addr);
    uint32_t tile_idx2 = h * n_tiles_width + (w + n_tiles_width_active/2);
    noc_async_read_tile(tile_idx2, src, cb_src_addr + tile_size_bytes);
    noc_async_read_barrier();
    cb_push_back(cb_in0, 2);
}

// Same as the writer kernel but inverse the direction
// * Calculate the 2D coordinate of the tensor (with batch folded in)
// * Convert to index in DRAM
// * Read from DRAM
uint32_t n_tiles_width_passive = n_tiles_width - n_tiles_width_active;
for(uint32_t passive_id = passive_begin; passive_id < passive_end; passive_id++) {
    uint32_t h = passive_id / n_tiles_width_passive;
    uint32_t w = passive_id % n_tiles_width_passive + n_tiles_width_active;
    uint32_t tile_idx = h * n_tiles_width + w;
    cb_reserve_back(cb_bypass, 1);
    uint32_t cb_bypass_addr = get_write_ptr(cb_bypass);
    noc_async_read_tile(tile_idx, src, cb_bypass_addr);
    noc_async_read_barrier();
    cb_push_back(cb_bypass, 1);
}

The kernels are getting guly. But heck they works. I am slightly worried about how much performance overhead the divisions are going to cause. It is slower, but we only gone from 18.16 to 18.8. As much I want to save the 640ns - I am good with it when most of the time is memory and there's path (making dimensions compile time constants) to reduce them, just now is too early to reduce that overhead.

Task scheduling

Now the fun problem of actually splitting the workload. Metalium provides split_work_to_cores as a part of it's SPMD infrastructure. Read the one of the official examples to understand how it works (link below). To describe briefly, split_work_to_cores tries it's best to divide given amount of work (an integer) into chunks that can be processed by each core while minimizing the imbalance of the number of work assigned to each core. The return values are as follows

• num_cores - Number of cores ended up being assigned some (i.e. > 0) work
• all_cores - Set of all cores assigned to the operation
• core_group_1 - Primary group of cores, each handling more work
• core_group_2 - Secondary group of cores, each handling less work (empty if the work divides evenly).
• work_per_core1 - Number of output tiles each core in the primary group processes.
• work_per_core2 - Number of output tiles each core in the secondary group processes (0 if the work divides evenly).

It might feel weird it returns two groups of cores, but that's more to handle the case where the work doesn't divide evenly then bad programming. For us, we use it to divvy up and assign each core some amount of active and passive tiles.

uint32_t active_tiles = D_activet/2 * Nt * B;
uint32_t passive_tiles = (Dt - D_activet) * Nt * B;

auto [num_cores_active,
    all_cores_active,
    core_group_1_active,
    core_group_2_active,
    work_per_core1_active,
    work_per_core2_active] =
    tt::tt_metal::split_work_to_cores(core_grid, active_tiles);

auto [num_cores_passive,
    all_cores_passive,
    core_group_1_passive,
    core_group_2_passive,
    work_per_core1_passive,
    work_per_core2_passive] =
    tt::tt_metal::split_work_to_cores(core_grid, passive_tiles);

Story doesn't end here. We have 2 assignments of cores and task. But we wish to execute the computation in a single kernel. We must tell Metalium that we wish to operate on the union of both core groups. Then during setting runtime argument, we tell each core how many work it needs to perform.

// Combine the two groups of cores
auto all_cores = all_cores_active.merge(all_cores_passive);

// Circular buffers are now associated with all cores used in the computation
// instead of a single core
//                                vvvvv
MakeCircularBufferFP32(program, all_cores, tt::CBIndex::c_0, 4);
MakeCircularBuffer(program, all_cores, tt::CBIndex::c_1, N*sizeof(int32_t), 32*sizeof(int32_t), tt::DataFormat::Int32);
MakeCircularBufferFP32(program, all_cores, tt::CBIndex::c_16, 4);
MakeCircularBufferFP32(program, all_cores, tt::CBIndex::c_17, 4);

// Likewise the compute kernels also are associated with all cores that is involved in the operation
//                                                                           vvvvvvvv
KernelHandle reader = CreateKernel(program, "../ttrope/kernels/reader.cpp", all_cores, DataMovementConfig{
    ...
});

KernelHandle writer = CreateKernel(program, "../ttrope/kernels/writer.cpp", all_cores, DataMovementConfig{
    ...
});

KernelHandle compute = CreateKernel(program, "../ttrope/kernels/compute.cpp", all_cores, ComputeConfig{
    ...
});

Again, Metalium, unlike OpenCL does not have built-in task identification. Instead, Metalium expects users to communicate with the core about what range of data to process. To do so we manually loop through all cores and assign them tasks based on their group membership.

uint32_t active_id = 0;
uint32_t passive_id = 0;
for(const auto& range : all_cores.ranges()) {
    for(const auto& core : range) {
        uint32_t active_size = 0;
        uint32_t passive_size = 0;

        // If the core should be processing active tiles
        if(core_group_1_active.contains(core)) {
            // Set the amount of work based the result of split_work_to_cores
            active_size = work_per_core1_active;
        }
        else if(core_group_2_active.contains(core)) {
            active_size = work_per_core2_active;
        }

        // Same for passive tiles
        if(core_group_1_passive.contains(core)) {
            passive_size = work_per_core1_passive;
        }
        else if(core_group_2_passive.contains(core)) {
            passive_size = work_per_core2_passive;
        }

        // Note that having active_size=0 (i.e. not in group) will result in active_begin
        // and active_end to have the same value - effectively skipping the loop (same for
        // passive tiles)
        //
        // Pass the work range to the core
        //                              vvvv
        SetRuntimeArgs(program, reader, core, std::vector<uint32_t>{(...,
            active_id, active_id+active_size, passive_id, passive_id+passive_size});
        SetRuntimeArgs(program, compute, core, std::vector<uint32_t>{...,
            active_id, active_id+active_size});
        SetRuntimeArgs(program, writer, core, std::vector<uint32_t>{(...,
            active_id, active_id+active_size, passive_id, passive_id+passive_size});

        // increment the counters to prepare for the next iteration of work assignment
        active_id += active_size;
        passive_id += passive_size;
    }
}

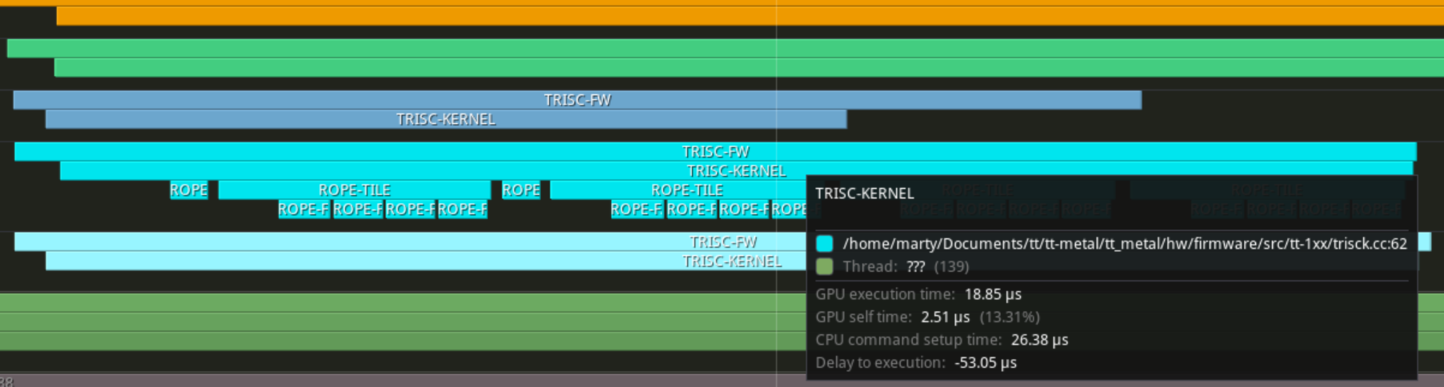
Run and boom! You can see on the profiler that multiple cores are now used during program run. Though now timing kernel execution is much harder as there are 56 cores to go through on my Wormhole N300. But after some scrolling, execution time for the compute kernel dropped to 7.02us and the overall time down to 10.2us. Not fast, fast. But expected given the majority of time is spent on compute.

That said, this scheme is not perfect. First, the two split_work_to_cores calls operate independently, which can lead to inefficiencies. If there is less work than the number of cores, both active and passive workloads may be assigned to the same cores, resulting in underutilized resources. Additionally, as shown in the screenshot above, even when there is more work than cores, the lack of coordination means split_work_to_cores assigns the same number of passive tiles to each core, regardless of whether that core is already handling active tiles. This creates inefficiencies, as cores not processing active tiles could take on more passive tiles than the current split allows.

Solving for these inefficiencies requires modeling the workload distribution and coordinating the active and passive workloads. This is achievable, and the optimization problem can be solved with relatively low latency using integer programming. Shaving even 2 microseconds off the current 10.2 microseconds of execution time would represent a 20% improvement. However, this optimization will have to wait for another day (or later), as there are more pressing issues to address.

Things tried that doesn't work

In theory, the current work assignment and scheduling scheme introduces another inefficiency. Even if there is enough workload to keep all cores busy multiple times, the current approach processes all active tiles first and then all passive tiles. This makes the kernel compute-bound initially and then memory-bound later.

For very large runs, such as B=32, N=2048, D=2048, D_active=256 (totaling 512MB of input tensor!), the overall execution time is approximately 5.8ms.

A simple solution in theory would be to interleave the active and passive processing. This way, the data movement kernel could feed the compute kernel some data, keep it busy for a while, and then fetch more data to copy the passive tiles. Rinse and repeat. However, no matter what I tried, this approach did not work. While a more even distribution of execution time was observed, the overall execution time always increased. The reason is unclear—perhaps it is due to the overhead of complex control flow or too many instructions causing the small instruction cache to be overwhelmed.

In any case, I tried, it didn’t work, and it’s not worth the time to debug further for now.

Supporting operating on a single row

Next, we move from pure Metalium mode to integrating it with TTNN. One issue we must address first is that our current implementation assumes the input to our kernels is always tile-aligned. This is primarily because Metalium lacks a padding utility, and I wanted to avoid writing one - what if I made a mistake and only discovered it when working in TTNN? However, for my goal, GGML will eventually require us to run RoPE on a single row of data, such as during inference. Fortunately, TTNN automatically pads tiled tensors to align with tile boundaries, and any padding values are discarded when converting back to row-major format. While operating on padding values would result in wasted compute, it is not a significant issue.

Though the position tensor is row-major and does not get padded, I cannot read 32 values as I am doing now when the tensor only has a size of 1. Some fixes are necessary. It's straightforward - just ensure I am reading from valid memory.

if(last_h != h) {
    uint32_t batch_active_tiles_wh = (n_tiles_width_active/2) * n_tiles_height;
    uint32_t b = active_id / batch_active_tiles_wh;
    cb_reserve_back(cb_in1, 1);
    uint32_t cb_idx_addr = get_write_ptr(cb_in1);
    uint32_t real_height = h%n_tiles_height;
    uint64_t read_addr = idx.get_noc_addr(b, 32*sizeof(int)*real_height);
    // Calculate and only read valid data out, up to 32 integers at a time
    uint32_t read_size = std::min(height_elements - real_height*32, uint32_t{32});
    noc_async_read(read_addr, cb_idx_addr, read_size*sizeof(int));
    noc_async_read_barrier();
    cb_push_back(cb_in1, 1);
    last_h = h;
}

Same story on the compute side. But since now the circular buffer could have size of 4 bytes (one integer) while rope_tile expects 32 valid values at all time. We just maintain a size 32 local array and copy what's in the circular buffer to it. So it never reads from potentially invalid memory.

int idxs[32];

...
for(uint32_t active_id=active_begin; active_id<active_end; active_id++) {
    ...
    if(last_h != h) {
        int* idxs_ptr = nullptr;
        if(need_pop) {
            cb_pop_front(cb_in1, 1);
        }
        cb_wait_front(cb_in1, 1);
        cb_get_tile(cb_in1, 0, &idxs_ptr);
        ... // same state managment as before

        uint32_t real_height = h%n_tiles_height;
        uint32_t valid_data_size = std::min(height_elements - real_height*32, uint32_t{32});
        memcpy(idxs, idxs_ptr, valid_data_size * sizeof(int));
        memset(idxs + valid_data_size, 0, (32 - valid_data_size) * sizeof(int));
    }
}

This change slightly reduces the speed but the gap is small enoguh that it can be ignroed.

Integrating into TTNN

This is the fun problem of gluing the kernel into TTNN's operator framework. There is official documentation (see link). But it is outdated and honestly it's easier to read the source code of simpler operators to figure out how that glue works - which is what I did. And I should update the TTNN operator bringup doc when I have time.

Each operator is a distinct type with an invoke method that serves as the entry point for the operation. For simplicity, the interface currently accepts two input tensors and an integer representing the active dimension size. The ttnn::register_operation function is then used to register the operator with TTNN. This wrapper handles basic sanity checks and facilitates integration, including support for TTNN profiling.

// Our own namespace for GGML operations
namespace ttggml {
using namespace ttnn;
struct RoPEOperation {
    static ttnn::Tensor invoke(const Tensor& src_tensor, const Tensor& index_tensor, uint32_t active_dim_size);
};

// Register the operation
constexpr auto rope = ttnn::register_operation<"ttggml::rope", ttggml::RoPEOperation>();
}

Then we create the glue that connects the TTNN framework to the Metalium backend. RoPEDeviceOperation provides four methods that TTNN uses to execute the operation on the device:

• compute_output_specs - Calculates the tensor specifications (size, shape, layout) in case allocation is required.
• create_output_tensors - Allocates tensors to be returned to the caller, if necessary.
• validate_with_output_tensors - Performs a sanity check to ensure the requested operation is supported.
• create_program - Creates the Metalium program that will be executed on the device.

In RoPEOperation::invoke, the tt::tt_metal::operation::run utility is called to initiate the operation. This utility handles kernel execution, program caching, and automatic operation state management. It maintains a table of device operations used to execute the operation on the device. If the same operation is reused (by hashing and comparing object value), the underlying program will be retrieved from the cache to avoid redundant creation.

struct RoPEDeviceOperation {
    const tt::tt_metal::MemoryConfig output_mem_config;
    const tt::tt_metal::DataType output_dtype{};
    const uint32_t active_dim_size = 0;

    // calculate the tensor specs (size, shape, layout)
    std::vector<ttnn::TensorSpec> compute_output_specs(
        const std::vector<Tensor>& input_tensors, const std::vector<std::optional<Tensor>>& output_tensors) const;

    // Allocate the output tensor if needed
    std::vector<Tensor> create_output_tensors(
        const std::vector<Tensor>& input_tensors, const std::vector<std::optional<Tensor>>& output_tensors) const;

    // Make sure the operation can run
    void validate_with_output_tensors(
        const std::vector<Tensor>& input_tensors, const std::vector<std::optional<Tensor>>& output_tensors) const;

    // Create the Metalium program (TTNN will be responsible for running it)
    tt::tt_metal::operation::ProgramWithCallbacks create_program(
        const std::vector<Tensor>& input_tensors, std::vector<Tensor>& output_tensors) const;
};

ttnn::Tensor ttggml::RoPEOperation::invoke(const Tensor& src_tensor, const Tensor& index_tensor, uint32_t active_dim_size) {
    return tt::tt_metal::operation::run(
        // the device operation object
        RoPEDeviceOperation{
            src_tensor.memory_config(),
            src_tensor.dtype(),
            active_dim_size
        },
        // input tensors
        {src_tensor, index_tensor},
        // optional input tensors
        {},
        // (pre-allocated) output tensors
        {})[0];
}

Implementing the device operation is relatively straightforward - creating the tensor, validating the operation, and setting up the program. Below is the source code for reference.

std::vector<ttnn::TensorSpec> ttggml::RoPEDeviceOperation::compute_output_specs(
    const std::vector<Tensor>& input_tensors, const std::vector<std::optional<Tensor>>& output_tensors) const
{
    // If we have pre-allocated output tnesor - just use that
    // Which we don't right now, but is easy to add later
    if (!output_tensors.empty() && output_tensors[0].has_value()) {
        return {output_tensors[0]->tensor_spec()};
    }

    const auto& input_tensor = input_tensors.at(0);
    return {TensorSpec(
        input_tensor.logical_shape(),
        tt::tt_metal::TensorLayout(
            output_dtype,
            input_tensor.layout(),
            output_mem_config)
        )
    };
}

std::vector<ttnn::Tensor> ttggml::RoPEDeviceOperation::create_output_tensors(
    const std::vector<Tensor>& input_tensors, const std::vector<std::optional<Tensor>>& output_tensors) const {
    // If we have pre-allocated output tnesor - just use that
    if (!output_tensors.empty() && output_tensors[0].has_value()) {
        return {output_tensors[0].value()};
    }

    // Else calculate the spec and create the tenstor on device
    const auto& input_tensor = input_tensors.at(0);
    auto spec = compute_output_specs(input_tensors, output_tensors)[0];
    return {create_device_tensor(spec, input_tensor.device())};
}

// The is largely the same validation logic as we had in the main program when writing in pure Metalium
// but ported to speak TTNN. If things doesn't look right - TT_FATAL throws exception and the user will
// see them in console output (or if on Python, the binding will translate it into Python errors)
void ttggml::RoPEDeviceOperation::validate_with_output_tensors(
    const std::vector<Tensor>& input_tensors, const std::vector<std::optional<Tensor>>& output_tensors) const {
    const auto& src_tensor = input_tensors.at(0);
    const auto& index_tensor = input_tensors.at(1);

    // expect src to have shape [batch, n_token, vec_dim]
    // expect index to have shape [batch, n_token]
    const auto& src_shape = src_tensor.logical_shape();
    const auto& index_shape = index_tensor.logical_shape();
    TT_FATAL(src_shape[-2] == index_shape[-1]
        && src_shape[-3] == index_shape[-2],
        "Shape mismatch: src_shape = {}, index_shape = {}. Expect format [batch, n_token, vec_dim] and [batch, n_token]", src_shape, index_shape);

    TT_FATAL(index_tensor.dtype() == tt::tt_metal::DataType::INT32, "Index tensor must be of type INT32");
    TT_FATAL(src_tensor.layout() == tt::tt_metal::Layout::TILE,  "Source tensor must be of layout TILE");
    TT_FATAL(index_tensor.layout() == tt::tt_metal::Layout::ROW_MAJOR,  "Index tensor must be of layout ROW_MAJOR");
    TT_FATAL(index_tensor.storage_type() == tt::tt_metal::StorageType::DEVICE, "Index tensor must be on device");
    TT_FATAL(src_tensor.storage_type() == tt::tt_metal::StorageType::DEVICE, "Source tensor must be on device");

    if (!output_tensors.empty() && output_tensors.at(0).has_value()) {
        const auto& out_tensor = output_tensors.at(0).value();
        TT_FATAL(out_tensor.logical_shape() == src_shape, "Output tensor shape must match source tensor shape");
        TT_FATAL(out_tensor.padded_shape() == src_tensor.padded_shape(), "Output tensor padded shape must match source tensor padded shape");
    }

    TT_FATAL(active_dim_size % 64 == 0, "active_dim must be a multiple of 64 (2 tiles)");
    TT_FATAL(active_dim_size <= src_tensor.padded_shape()[-1], "active_dim must be less than the last dimension of the source tensor");
}

create_program is the basically the main program written earlier, driving Metalium itself. Setting up programs, creating kernel and work scheduling. Won't paste the full code here, you get the point.

tt::tt_metal::operation::ProgramWithCallbacks ttggml::RoPEDeviceOperation::create_program(
    const std::vector<Tensor>& input_tensors, std::vector<Tensor>& output_tensors) const
{
    tt::tt_metal::Program program{};
    const auto& src_tensor = input_tensors.at(0);
    const auto& index_tensor = input_tensors.at(1);
    const auto& output_tensor = output_tensors.at(0);

    // Glue TTNN into our Metalim code (minus the validation since it's done in validate_with_output_tensors)
    const uint32_t B = src_tensor.logical_shape()[-3];
    const uint32_t D = src_tensor.logical_shape()[-1];
    const uint32_t D_active = active_dim_size;
    const uint32_t N = src_tensor.logical_shape()[-2];

    // We used to only program for FP32. TTNN can have different input types. Need to handle different circular buffers
    MakeCircularBuffer(program, all_cores, tt::CBIndex::c_0, 4, src_tensor.dtype());
    MakeCircularBuffer(program, all_cores, tt::CBIndex::c_1, 2*32*sizeof(int32_t), 32*sizeof(int32_t), DataFormat::Int32);
    MakeCircularBuffer(program, all_cores, tt::CBIndex::c_16, 4, output_tensor.dtype());
    MakeCircularBuffer(program, all_cores, tt::CBIndex::c_17, 4, src_tensor.dtype());

    ...

    auto override_runtime_args_callback = [reader, writer, all_cores](
                                                  const void* operation,
                                                  Program& program,
                                                  const std::vector<Tensor>& input_tensors,
                                                  const std::vector<std::optional<const Tensor>>&,
                                                  const std::vector<Tensor>& output_tensors) {
            auto src_buffer = input_tensors.at(0).buffer();
            auto idx_buffer = input_tensors.at(1).buffer();
            auto dst_buffer = output_tensors.at(0).buffer();

            for(const auto& range : all_cores.ranges()) {
                for (const auto& core : range) {
                    {
                        auto& runtime_args = GetRuntimeArgs(program, reader, core);
                        runtime_args[0] = src_buffer->address();
                        runtime_args[4] = idx_buffer->address();
                    }

                    {
                        auto& runtime_args = GetRuntimeArgs(program, writer, core);
                        runtime_args[0] = dst_buffer->address();
                    }
                }
            }
        };

        return {std::move(program), override_runtime_args_callback};
}

As discussed earlier, TTNN is quite efficient at reusing already created programs. It maintains a table of device operation objects (like RoPEDeviceOperation in our case) and performs a lookup whenever an operation is requested. If the operation has been created before, it simply invokes override_runtime_args_callback to update the tensor addresses, signaling, "The exact operation I need already has a program."

However, since the lookup is based on the operation object, it can sometimes lead to unnecessary object creation. For example, n_dim_active is a runtime argument to the kernel, but changing it will trigger a program recreation. That said, there is an additional layer of kernel caching based on the actual kernel and compile-time arguments, which prevents kernel recompilation in such cases. So, while the overhead isn't great - just a redo of work scheduling - it can still be optimized. To minimize this overhead, you can implement a compute_program_hash method that includes only the relevant parameters in the hash calculation.

Anyway, we can test the interaction and invocation using high level TTNN API now.

int main()
{
    auto device = ttnn::open_mesh_device(0);
    auto src = ttnn::ones(ttnn::Shape({1, 32, 2048}), DataType::FLOAT32, Layout::TILE, *device);
    auto idx = ttnn::ones(ttnn::Shape({1, 32}), DataType::INT32, Layout::ROW_MAJOR, *device);
    auto res = ttggml::rope(src, idx, 256); // invoke our operation!
    std::cout << res.write_to_string() << std::endl;

    device->close();
}

Which prints the following in the console.

ttnn.Tensor([[[-0.3011, -0.2046,  ...,  1.0000,  1.0000],
              [-0.3011, -0.2046,  ...,  1.0000,  1.0000],
              ...,
              [-0.3011, -0.2046,  ...,  1.0000,  1.0000],
              [-0.3011, -0.2046,  ...,  1.0000,  1.0000]]], shape=Shape([1, 32, 2048]), dtype=DataType::FLOAT32, layout=Layout::TILE)

Hooray! It works!

Support changing base frequency

Though the original RoPE paper and most models use a frequency base of 10000, some models opt for a different base frequency. Supporting this is straightforward, but there’s one small issue: we currently hard-code the logarithm of the frequency (thanks to the math tricks needed to make the operation efficient on-device), and we really don’t want to perform floating-point calculations, especially log, on softfp.

In typical OpenCL fashion - the Metalium API was initially designed to look like OpenCL. We just let the host do the math and add a define.

I also tried to delete the floating point division by making it a compile time value. Don't know what the compiler is doing, but the performance has a small but statistically significant decrease.

std::map<std::string, std::string> defines;
defines["FREQ_BASE"] = std::to_string(freq_base);
defines["FREQ_BASE_LOG"] = std::to_string(std::log(freq_base));
// defines["INV_D_ACTIVE_2"] = float(2.f / D_active); // don't know why this make things slower.

KernelHandle reader = CreateKernel(program, "../ttrope/kernels/reader.cpp", all_cores, DataMovementConfig{
    ...
    .defines = defines
});
// no need to add defines to data movement kenrels

Integrating into GGML

Finally, I’ve reached the stage where I can tackle the original problem I set out to solve. The GGML backend is essentially a giant switch-case system: one part determines what the backend supports, and another part dispatches operations to the appropriate handler.

static bool ggml_backend_metalium_can_rope(const struct ggml_tensor * dst)
{
    // Extract the parameters from the tensor's parameter pack
    std::array<int32_t, 5> int_params;
    memcpy(int_params.data(), dst->op_params, sizeof(int_params));
    auto [ n_past, n_dims, mode, n_ctx, n_ctx_orig ] = int_params;
    std::array<float, 6> float_params;
    memcpy(float_params.data(), dst->op_params + int_params.size() , sizeof(float_params));
    auto [ freq_base, freq_scale, ext_factor, attn_factor, beta_fast, beta_slow ]
         = float_params;

    // Check that the requested operation is supported by our implementation
    // - NeoX mode
    // - Not doing YaRN
    return (n_dims % 64 == 0 && mode == GGML_ROPE_TYPE_NEOX)
        && freq_scale == 1
        && ext_factor == 0
        && attn_factor == 1
        && dst->src[2] == nullptr; // Don't support freq factor
}

Invoking RoPE looks similar, but this time we call the new operator directly. TensorWithMeta is an outdated legacy data structure that really needs to be replaced - please excuse the mess.

static void ggml_backend_metalium_rope(ggml_backend_metalium_context * ctx, struct ggml_tensor * dst)
{
    GGML_UNUSED(ctx);

    TensorWithMetadata* dst_meta = (TensorWithMetadata*)dst->extra;
    TensorWithMetadata* src_meta = (TensorWithMetadata*)dst->src[0]->extra;

    std::array<int32_t, 5> int_params;
    memcpy(int_params.data(), dst->op_params, sizeof(int_params));
    auto [ n_past, n_dims, mode, n_ctx, n_ctx_orig ] = int_params;
    // Don't support any of the params in the FP section yet

    // Invoke the operation we just wrote!
    auto res = ttggml::rope(
        *realize_ggml_view(dst->src[0]),Because no sane person will be doing multi thousand batch
        *realize_ggml_view(dst->src[1]),
        n_dims);

    *dst_meta = {
        .tensor = std::make_shared<tt::tt_metal::Tensor>(std::move(res)),
        .ggtype = dst->type,
        .bufctx = src_meta->bufctx
    };
}

And this is where I figured out I made the astronmical scale blunder. Trying to run GGML unit tests shows error:

Shape mismatch: src_shape = [2, 1, 64], index_shape = [2]. Expect format [batch, n_token, vec_dim] and [batch, n_token]

Fuck.

Turns out in my original test code I have set N to 1 which happens to be the implied default dimenstion size. And GGML actually wants per btach positions. Argh+(_S#)@U@(*)!!!!!!!!!

Fine. Let's deal with that mistkae.

For simplicity, I'll drop the per-32 positions approach and just DMA the entire position array. No big deal - nobody in their right mind is running RoPE with a batch size anywhere near 1000. Something else will break long before RoPE does. The circular buffer for the indices now matches the size of the entire position tensor:

MakeCircularBuffer(program, all_cores, tt::CBIndex::c_1, B*sizeof(int32_t), B*sizeof(int32_t), DataFormat::Int32);

And we can get rid of the row tracking in both the reader and compute kernel. What's needed now is just one big read at the beginning and waiting for that read.

// reader.cpp

// Read all of the position array into SRAM at once
cb_reserve_back(cb_in1, 1);
uint32_t cb_idx_addr = get_write_ptr(cb_in1);
uint64_t read_addr = idx.get_noc_addr(0, 0);
noc_async_read(read_addr, cb_idx_addr, batch_size*sizeof(int));
noc_async_read_barrier();
cb_push_back(cb_in1, 1);

for(uint32_t active_id=active_begin; active_id<active_end; active_id++) {
    ...
    // rest of the reader code

// compute.cpp

// Wait for reader to read in the positions
int* idxs_ptr = nullptr;
cb_wait_front(cb_in1, 1);
cb_get_tile(cb_in1, 0, &idxs_ptr);
idxs_ptr += 4;

for(uint32_t active_id=active_begin; active_id<active_end; active_id++) {
    ...
    // rest of the compute code

And rewriting constraint testing later... it works! GGML unit tests shows stuff are passing.

As a side benifit of having per-batch position. The compitation can be vastly simplified. Instead of storing per-column precomputed exponent and per-row indices. Even the (less but stil quite) expensive sine function can be hoisted out of the inner loop.

inline void rope_face(int pos, int face_idx, int pos_in_vector)
{
    // No more expensive trigonometric and exponential calls in the acutal compute
    int face_col = face_idx % 2;
    int dst_offset = face_idx*8;
    for (int h = 0; h < 2; h++) {
        vFloat sin_value = dst_reg[64+face_col*2+h];   // load shared sine and cosine
        vFloat cos_value = dst_reg[64+face_col*2+h+4];
        for (int i = 0; i < 4; i++) {
            int idx = i*2+h;
            vFloat x = dst_reg[dst_offset+idx];
            vFloat y = dst_reg[dst_offset+idx+32];
            dst_reg[dst_offset+idx] = x * cos_value - y * sin_value;
            dst_reg[dst_offset+idx+32] = x * sin_value + y * cos_value;
        }
    }
}

inline void rope_tile(int pos, float inv_d, int vec_offset)
{

    // Expensive calls are now shared across faces within a tile.
    for(int i=0;i<4;i++) {
        int internal_offset = ((i / 2 == 0) ? 0 : 16);
        int pos_in_vector = vec_offset + internal_offset;
        vFloat block_lane_id = int32_to_float((vConstTileId & 15) + (pos_in_vector + i % 2));
        vFloat exponent = block_lane_id * vConstFloatPrgm2;

        vFloat term_to_exp = -exponent * vConstFloatPrgm0 - vConstFloatPrgm1;
        vFloat freq = vector_exp(term_to_exp);

        vFloat vpos = int32_to_float(pos);
        vFloat angle_phase = vpos * freq;
        vFloat sin_value = vector_sin_phase(angle_phase) * mscale;
        vFloat cos_value = vector_sin_phase(0.5f - angle_phase) * mscale;
        // store the sine and cosine values in the reserved dst_reg area
        dst_reg[64+i] = sin_value;
        dst_reg[64+i+4] = cos_value;
    }

    ...
    // Rest of rope_tile
}

Arguably it's a different algorithm now. But benchmarking it shows that we are down to 10us of compute time to RoPE for N=32 D_active=256. Pretty nice.

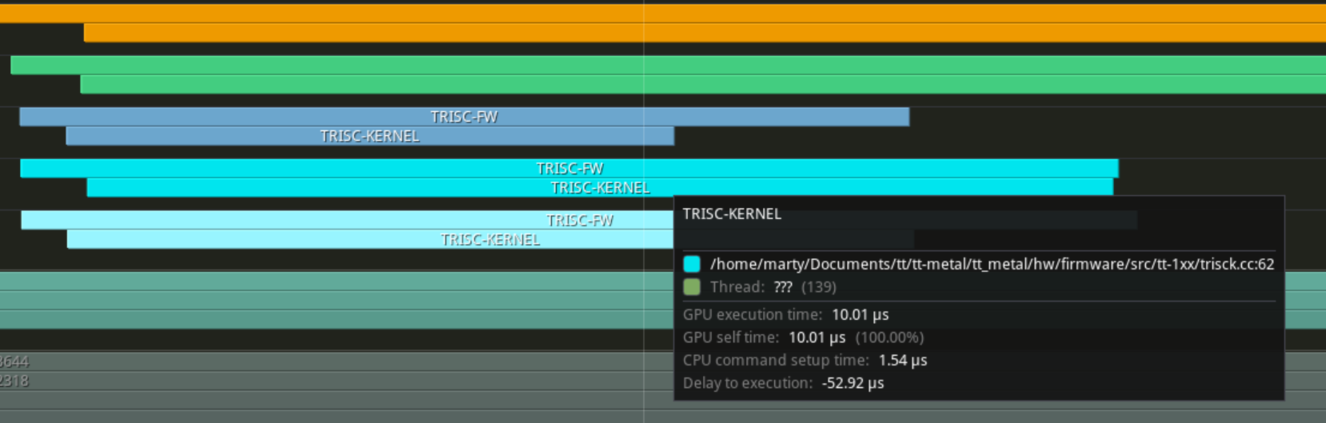
YaRN

At this point, I’m seeing how much faster LLMs are with RoPE offloaded. Gemma 2 and 3 both use the NeoX variant of RoPE, so I gave it a shot. The results? They are incoherent. Why can’t I ever have nice things? Dumped some parameters and noticed beta_fast and beta_slow are set. Could it be missing YaRN support? But the unit tests pass. What...?

I’ve looked at GGML's CPU and OpenCL code for RoPE before - and immediately noped out of there. I really didn’t want to dive in and learn it. 🤦

YaRN is a technique that extends the context window beyond what the model was originally trained for. Remember how we got the original LLaMA to handle a 8K context window? That was thanks to YaRN.

I spent an entire night trying to avoid reading GGML's code. Instead, I consulted various LLMs and read blog posts, attempting to piece together how YaRN works. After many failed attempts and falling asleep multiple times, I finally got tought and is ready to read the OpenCL kernel. Turns out, it’s not that bad - especially after already nailing the basic version of RoPE. In the OpenCL backend, the kernel_rope_neox_f32 function is written as follows:

// yanked from rope.cl
float2 corr_dims = rope_yarn_corr_dims(n_dims, n_ctx_orig, freq_base, beta_fast, beta_slow);
...
if (i0 < n_dims) {
    int ic = i0/2;

    const float theta = theta_base * pow(freq_base, inv_ndims*i0);

    const float freq_factor = src2 != src0 ? src2[ic] : 1.0f;

    float2 cos_sin_theta = rope_yarn(theta/freq_factor, freq_scale, corr_dims, i0, ext_factor, attn_factor);

    global float * src      = (global float *)((global char *) src0 + i3*nb03 + i2*nb02 + i1*nb01 + ic*nb00);
    global float * dst_data = (global float *)((global char *)  dst + i3*nb3  + i2*nb2  + i1*nb1  + ic*nb0);

    const float x0 = src[0];
    const float x1 = src[n_dims/2];

    dst_data[0]        = x0*cos_sin_theta.s0 - x1*cos_sin_theta.s1;
    dst_data[n_dims/2] = x0*cos_sin_theta.s1 + x1*cos_sin_theta.s0;
}

Ok.. that's familare. We did the same math. Did not support freq_factor so that's a constant 1.0. rope_yarn_corr_dims and rope_yarn is interesting. But otherwise it is just reading the two values in and apply the rotation. The mistery functions are quite reasonable too. rope_yarn seems to be using what rope_yarn_corr_dims calculated and applying transformation to them.

// yanked from rope.cl
float rope_yarn_ramp(float low, float high, int i0) {
    const float y = (i0 / 2 - low) / max(0.001f, high - low);
    return 1.0f - min(1.0f, max(0.0f, y));
}
float2 rope_yarn(
    float theta_extrap, float freq_scale, float2 corr_dims, int i0, float ext_factor, float mscale
) {
    // Get n-d rotational scaling corrected for extrapolation
    float theta_interp = freq_scale * theta_extrap;
    float theta = theta_interp;
    if (ext_factor != 0.0f) {
        float ramp_mix = rope_yarn_ramp(corr_dims.s0, corr_dims.s1, i0) * ext_factor;
        theta = theta_interp * (1 - ramp_mix) + theta_extrap * ramp_mix;

        // Get n-d magnitude scaling corrected for interpolation
        mscale *= 1.0f + 0.1f * log(1.0f / freq_scale);
    }
    return (float2)(cos(theta) * mscale, sin(theta) * mscale);
}

rope_yarn_corr_dims is complicated and involves lots of divisions and logarithmics. This is problematic.. the SFPU can't do division and I will have to approximate the logarithm. Please not another numerical nightmatre I have to deal with.

// Apparently solving `n_rot = 2pi * x * base^((2 * max_pos_emb) / n_dims)` for x, we get
// `corr_fac(n_rot) = n_dims * log(max_pos_emb / (n_rot * 2pi)) / (2 * log(base))`
float rope_yarn_corr_factor(int n_dims, int n_ctx_orig, float n_rot, float base) {
    return n_dims * log(n_ctx_orig / (n_rot * 2 * M_PI_F)) / (2 * log(base));
}

float2 rope_yarn_corr_dims(
    int n_dims, int n_ctx_orig, float freq_base, float beta_fast, float beta_slow
) {
    // start and end correction dims
    return (float2)(
        max(0.0f,         floor(rope_yarn_corr_factor(n_dims, n_ctx_orig, beta_fast, freq_base))),
        min(n_dims - 1.0f, ceil(rope_yarn_corr_factor(n_dims, n_ctx_orig, beta_slow, freq_base)))
    );
}

Luckily, everything rope_yarn_corr_dims needs is available on the host and outputs two floating-point numbers. I can simply perform the calculations on the host and pass the results to the SFPU via defines at kernel build time. So that's exactly what I did. Conveniently, GGML already provides ggml_rope_yarn_corr_dims in one of its headers.

Looking at the logic of rope_yarn, each of the factors and scales appears to act as an identity under certain conditions. This means I can make them conditional - only including them when their effect on the final output is nontrivial. As we've seen, loading constants on the SFPU isn't free, and I've already maxed out the available constant registers. On the host side, the defines (and precomputed values) are only generated when the factors actually influence the final result.

if(attn_factor != 1.f) {
    defines["ATTN_FACTOR"] = to_string_precise(attn_factor);
}
if(freq_scale != 1.f) {
    defines["FREQ_SCALE"] = to_string_precise(freq_scale);
    defines["LOG_1_FREQ_SCALE"] = to_string_precise(std::log(1.0f / freq_scale));
}
if(ext_factor != 0.f) {
    defines["EXT_FACTOR"] = to_string_precise(ext_factor);
    float corr_dims[2];
    ggml_rope_yarn_corr_dims(D_active, n_ctx_orig, freq_base, beta_fast, beta_slow, corr_dims);
    // In case we get garbage
    if(isinf(corr_dims[0]) || isnan(corr_dims[0])) {
        corr_dims[0] = 0;
    }
    if(isinf(corr_dims[1]) || isnan(corr_dims[1])) {
        corr_dims[1] = 0;
    }
    defines["CORR_DIMS0"] = to_string_precise(corr_dims[0]);
    defines["CORR_DIMS1"] = to_string_precise(corr_dims[1]);
}

Device-side, I expanded the logic of rope_yarn and added some #ifdefs to make the code more efficient. Luckily, no new softfp calculations were needed. The only remaining division on the device has all its parameters as compile-time constants - the optimizer should be able to handle this and optimize it away.

#ifdef EXT_FACTOR
sfpi_inline vFloat rope_yarn_ramp(vFloat vec_pos) {
    vFloat y = (vec_pos - CORR_DIMS0) * (1.f / std::max(0.001f, float(CORR_DIMS1 - CORR_DIMS0)));
    v_if(y < 0.f) {
        y = 0;
    }
    v_elseif(y > 1.f) {
        y = 1;
    }
    v_endif;
    return 1.f - y;
}
#endif

for(int i=0;i<4;i++) {
    int internal_offset = ((i / 2 == 0) ? 0 : 16);
    int pos_in_vector = vec_offset + internal_offset;
    vFloat block_lane_id = int32_to_float((vConstTileId & 15) + (pos_in_vector + i % 2));
    vFloat exponent = block_lane_id * vConstFloatPrgm2;

    vFloat term_to_exp = -exponent * vConstFloatPrgm0 - vConstFloatPrgm1;
    vFloat freq = vector_exp(term_to_exp);

    vFloat freq_scaled = freq;
    vFloat mscale = 1.f;
    #ifdef FREQ_SCALE
        freq_scaled = freq * FREQ_SCALE;
    #endif
    #ifdef ATTN_FACTOR
        mscale = ATTN_FACTOR;
    #endif
    vFloat theta = freq_scaled;
    // enable YaRN if needed
    #ifdef EXT_FACTOR
        vFloat ramp_mix = rope_yarn_ramp(block_lane_id) * EXT_FACTOR;
        theta = freq_scaled * (1 - ramp_mix) + freq * ramp_mix;
        #ifdef LOG_1_FREQ_SCALE
            mscale *= 1.0f + 0.1f * LOG_1_FREQ_SCALE;
        #endif // else mscahe *= 1 (the other half collasps to 0) - does nothing
    #endif

    vFloat vpos = int32_to_float(pos);
    vFloat angle_phase = vpos * theta;
    vFloat sin_value = vector_sin_phase(angle_phase) * mscale;
    vFloat cos_value = vector_sin_phase(0.5f - angle_phase) * mscale;
    dst_reg[64+i] = sin_value;
    dst_reg[64+i+4] = cos_value;
}

And that's YaRN. Unit tests passing. But Gemma is still incoherent. What the actualy...

"Normal" RoPE

Hours staring at the output of llama-eval-callback and trying to figure how what my RoPE is doing wrong. Values looks correct and the unit tests passes. I decided I need to test on a simpler model. Usually I use TinyLLaMA for debuging. But that uses the normal variant not NeoX. Fine... I will write that kernel.

The normal variant is the interleaving one mentioned earlier. GGML's behaivour can be verified against our original reference code with some simple modifications. Changing loading and storing data not half of D_active across, but next to it. The change is trivial.

std::vector<float> rope_normal(const std::vector<float>& vec, const std::vector<int>& pos, int D, int D_active)
{
    size_t rotate_dim = D_active == -1 ? vec.size() : D_active;
    assert(D_active % 2 == 0 && "Active dimension must be even");
    assert(D_active <= D && "Active dimension must be less than or equal to total dimension");
    std::vector<float> result(vec.size());
    size_t n = pos.size();
    for(size_t n = 0; n < N; ++n) {
        size_t offset = n * D;
        for (size_t i = 0; i < D_active/2; i ++) {
            float exponent = 2.f * (float)i / D_active;
            float freq = 1.0f / std::pow(10000.0f, exponent);

            float angle = pos * freq;
            float cos_angle = std::cos(angle);
            float sin_angle = std::sin(angle);

            // was
            // float x = vec[offset + i];
            // float y = vec[offset + i + D_active/2];
            // new - the "normal" RoPE
            float x = vec[offset + i * 2];
            float y = vec[offset + i * 2 + 1];

            // result[offset + i] = x * cos_angle - y * sin_angle;
            // result[offset + i + D_active/2] = x * sin_angle + y * cos_angle;
            result[offset + i * 2] = x * cos_angle - y * sin_angle;
            result[offset + i * 2 + 1] = x * sin_angle + y * cos_angle;
        }

        for (size_t i = D_active; i < D; i++) {
            result[offset + i] = vec[offset + i];
        }
    }
    return result;
}

Recall that the SFPU loads lanes in an interleaved manner. This interleaving is what makes the normal variant feasible on the SFPU. We want to load from vec[offset + i * 2] and vec[offset + i * 2 + 1] into seperate values. The interleaving makes, loading (and storing) from dst_reg[offset + i * 2] and dst_reg[offset + i * 2 + 1] naturally produces the desired result.

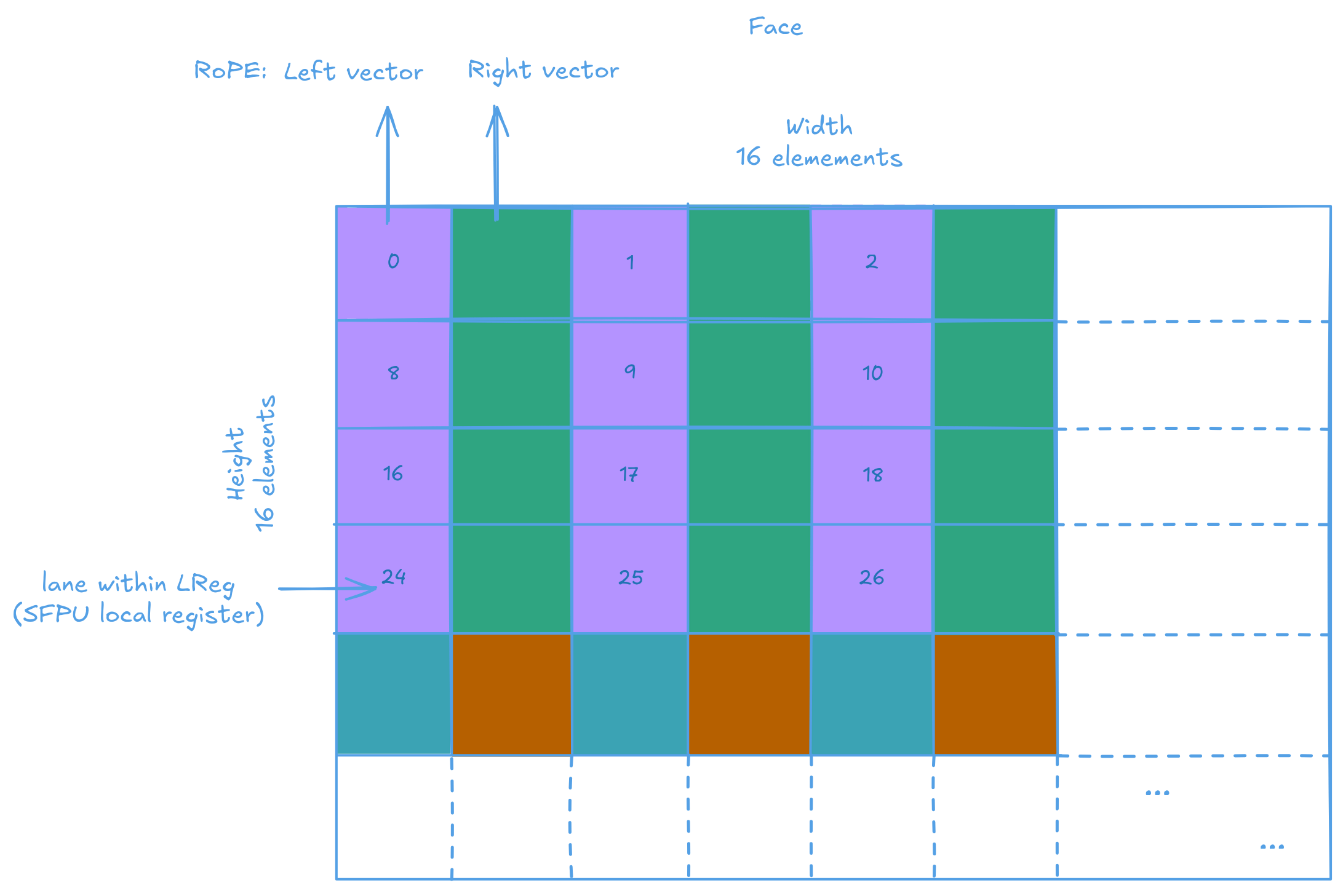
The reader and writer also have to be changed. Now they don't read/write 2 tiles from D_activet apart. Instead they do one time at a time from the active reagon. Change is trivial and overall leads to supporting a minimal active dimension size of 32 (and potentially down to 16, but that's extra code and I don't see any model needing it).

// normal_reader.cpp
// Reading a single tile at a time in active reagon. Same for the writer
for(uint32_t active_id=active_begin; active_id<active_end; active_id++) {
    uint32_t h = active_id / n_tiles_width_active;
    uint32_t w = active_id % n_tiles_width_active;

    cb_reserve_back(cb_in0, 1);
    uint32_t cb_src_addr = get_write_ptr(cb_in0);
    uint32_t tile_idx =  h * n_tiles_width + w;
    noc_async_read_tile(tile_idx, src, cb_src_addr);
    noc_async_read_barrier();
    cb_push_back(cb_in0, 1);
}

// normal_compute.cpp
// Now waits for and produces a single tile at a time
for(uint32_t active_id=active_begin; active_id<active_end; active_id++) {
    uint32_t b = active_id / n_tiles_width_active / n_tiles_height;
    uint32_t w = active_id % n_tiles_width_active;
    cb_wait_front(cb_in0, 1);
    tile_regs_acquire();

    copy_tile(cb_in0, 0, 0);
    MATH(rope_tile(idxs_ptr[b], inv_d, w*32));
    tile_regs_commit();
    tile_regs_wait();

    cb_reserve_back(cb_out0, 2);
    pack_tile(0, cb_out0, 0);
    tile_regs_release();
    cb_push_back(cb_out0, 1);
    cb_pop_front(cb_in0, 1);
}

Because the "normal" variant processes a tile at a time, instead of a pair. The total unit of work is increased by a factor of 2. Though the total amount of work does not change.

// NeoX processes tiles a pair at a time so the total work amount is cut in half. But each unit of work
// takes twice as long.
uint32_t active_tiles = rope_type == ttggml::RoPEType::NeoX ? D_activet/2 * Nt * B : D_activet * Nt * B;
uint32_t passive_tiles = (Dt - D_activet) * Nt * B;
auto [num_cores_active,
    all_cores_active,
    core_group_1_active,
    core_group_2_active,
    work_per_core1_active,
    work_per_core2_active] =
    tt::tt_metal::split_work_to_cores(core_grid, active_tiles);
auto [num_cores_passive,
    all_cores_passive,
    core_group_1_passive,
    core_group_2_passive,
    work_per_core1_passive,
    work_per_core2_passive] =
    tt::tt_metal::split_work_to_cores(core_grid, passive_tiles);

That's it. The "Normal" RoPE operation is now supported and working.

However, even TinyLLaMA is having troubles running and crashing with NaN detected. Much debugging later I found the problem is unrelated largely. After fixing, LLMs are acting correcly. Overall providing a 10% performance improvement - mostly stemming from reduced need to move data between accelerator and host to use the CPU as fallback.

I can optimize ther kernel further. But I'll call it good enough and try getting other missing operations working. Beeing reading on FlashAttention lately

Supporting frequency factors

Final missing piece of the puzzle, with normal RoPE implementeted, GGML still rejects running RoPE for LLaMA 3.1 due to an additional tensor attached to the operation - the frequency factor. It is easy to undersand what the parameter does by reading the OpenCL kernel.

// ic is the pair index
int ic = i0/2;

// GGML's way of hacking and not putting NULL into src2
float freq_factor = src2 != src0 ? src2[ic] : 1.0f;

// divide the frequency by freq_factor
float2 cos_sin_theta = rope_yarn(theta/freq_factor, freq_scale, corr_dims, i0, ext_factor, attn_factor);

Sounds easy enough. For the NeoX variant we just load a new tensor and load from the first (logical) row of... ohh... SFPU loads works loading 4 rows at a time. I could manually broadcast the values using the reader kernel. But the RISC-V cores are slow and does not have much bandwidth to SRAM. I asked around internally and apparently the SFPTRANSP instruction can be abused into broadcasting values across lanes.

I have stolen the documentation's explnation image. It takes 4 registers and collect the i-th row of each into the i-th register.

Luckliy SFPI provides a wrapper for this instruction, no need to drop down to the TTI macro level of programming (TTI_* are macros that allows direct assembly level programming without actually writing assembly). To use the wrapper:

vFloat d0 = set_to_some_value();
vFloat d1 = ff;
vFloat d2 = ff;
vFloat d3 = ff;
sfpi::subvec_transp(d0, d1, d2, d3);

With that, for NeoX RoPE, adding support for freq_factor is simply reading a new tile in the reader

#ifdef HAS_FREQ_FACTOR
    cb_reserve_back(cb_in2, 1);
    uint32_t ff_idx = w;
    uint32_t cb_ff_addr = get_write_ptr(cb_in2);
    noc_async_read_tile(ff_idx, ff, cb_ff_addr);
#endif

noc_async_read_barrier();
...
#ifdef HAS_FREQ_FACTOR
    cb_push_back(cb_in2, 1);
#endif

And loaded into tile 3 by the compute kernel

#ifdef HAS_FREQ_FACTOR
    cb_wait_front(cb_in2, 1);
#endif

...
#ifdef HAS_FREQ_FACTOR
    copy_tile_init(cb_in2);
    copy_tile(cb_in2, 0, 3);
#endif

...
#ifdef HAS_FREQ_FACTOR
    cb_pop_front(cb_in2, 1);
#endif

Then broadcast the first row and inverse it before in order to effectively divide the frequency by the frequency factor (the SFPU does not support division). I did run into a problem there the compiler failed to allocate SFPU registers. I just have to use Dst as storage again. This time tile to 3 (because it is used to store the frequency factor, so I can safely use it as I know no one else will use it, that said I could have used the extra space in tile 2 that is left).

_reciprocal_compat_ is a function I yanked from other places in the Metalium LLK library. The original implementation requires vConstFloatPrgm0 to be set to 2.0 - which I am using for the inverse of log. So I made a copy and replaced the use of constant registers. And it doesn't handle negative numbers correctly.

#ifdef HAS_FREQ_FACTOR
// Seperate computation of inverse of freq_factor as otherwise SFPI fails to compile due to
// failing to allocate registers
for(int i=0;i<4;i++) {
    // we want to read the 1st vector of face 0 and 1 (logically the 1st row)
    int ff_idx = 96+(i%2)+(i/2*8);
    vFloat ff = vFloat(dst_reg[ff_idx]);
    vFloat d0 = ff;
    vFloat d1 = ff;
    vFloat d2 = ff;
    vFloat d3 = ff;
    sfpi::subvec_transp(d0, d1, d2, d3);
    vFloat r = _reciprocal_compat_<4>(d0);
    v_if(ff < 0) {
        r = -r;
    }
    v_endif;
    dst_reg[ff_idx] = r;
}
#endif

...

// Later on calculating the frequency
#ifdef HAS_FREQ_FACTOR
    int ff_idx = 96+(i%2)+(i/2*8);
    freq = freq * vFloat(dst_reg[ff_idx]);
#endif

The "Normal" variant is more troublesome. Though SFPU's interleaved load made it possible to apply the rotation pairwise within a tile. The kernel actually needs to load conseqtive elements from the frequency factor tensor as the scaling is applied to the overall pair.

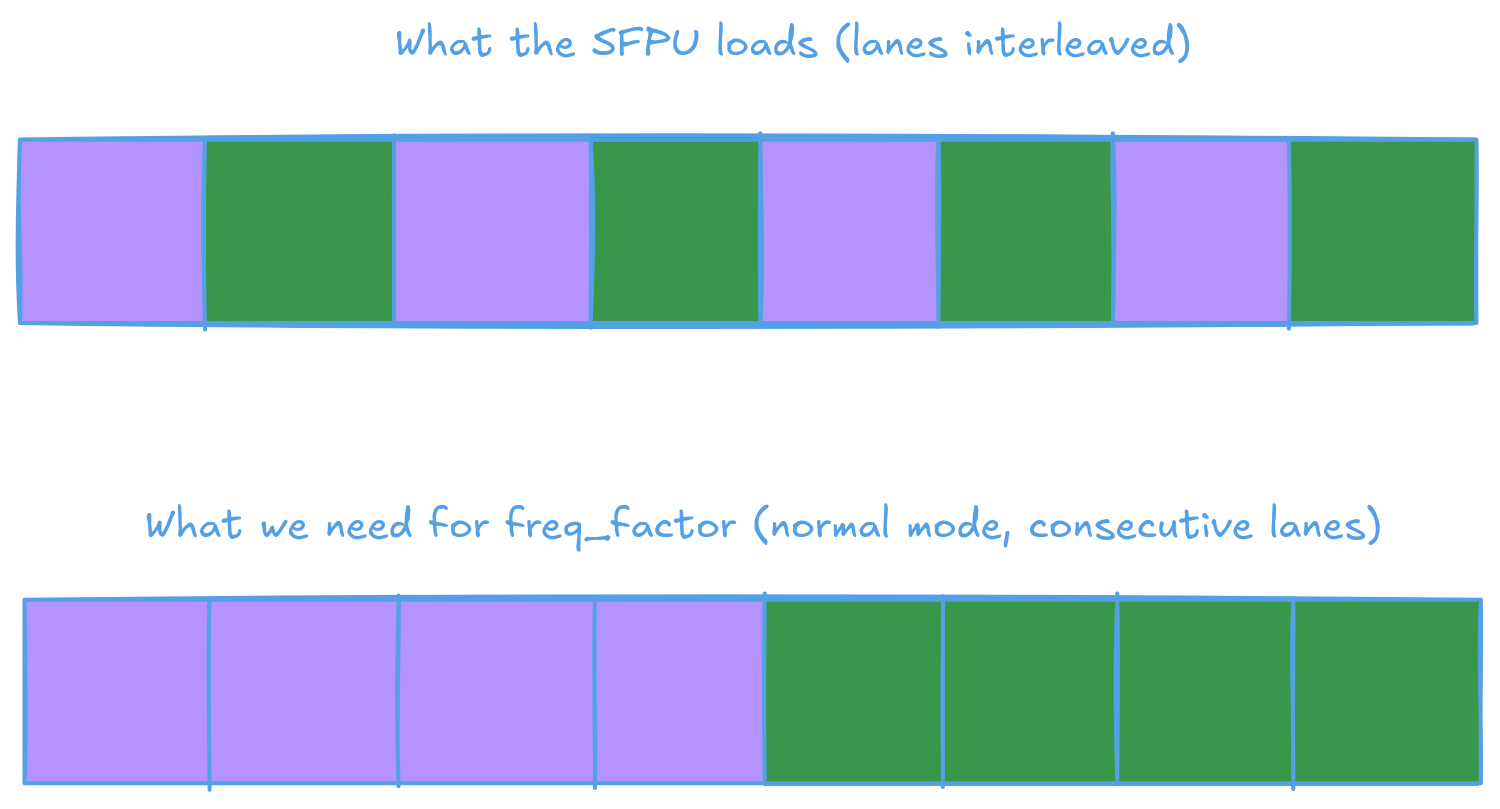
Unfortunately I can't come up with a clearver solution this time. The only way I can think of is to get the reader kernel to permute the frequency factor tensor to make the SFPU load the right elements. Oh and because unlike NeoX, each tile only consumes half of the frequency factor tensor read. The kernel also needs to keep track when to read in new tiles of the frequency factor tensor.

#ifdef HAS_FREQ_FACTOR
    // Half a tile is consumed per "normal" rope operation - update every 2 tile
    uint32_t ff_idx = w/2;
    bool read_ff = last_ff_idx != ff_idx;
    uint32_t cb_ff_addr = 0;
    if(read_ff) {
        cb_reserve_back(cb_in2, 1);
        cb_ff_addr = get_write_ptr(cb_in2);
        noc_async_read_tile(ff_idx, ff, cb_ff_addr);
        last_ff_idx = ff_idx;
    }
#endif

...
noc_async_read_barrier();
#ifdef HAS_FREQ_FACTOR
if(read_ff) {
    unsigned short* ff_ptr = (unsigned short*)cb_ff_addr;
    // Permute frequency factor tensor to match the SFPU load pattern
    // Applies to the 1st row of face 0 and face 1
    for(int i=0;i<2;i++) {
        unsigned short buf[16];
        // 256 = number of elements per face. Using short because
        // I intend the kernel holds BFLOAT16. Which is 16bits wide
        unsigned short* ptr = ff_ptr + i * 256;
        for(int j=0;j<16;j++) {
            buf[j] = j%2 == 0 ? ptr[j/2] : ptr[j/2+8];
        }
        memcpy(ptr, buf, sizeof(buf));
    }
    cb_push_back(cb_in2, 1);
}
#endif

Compute kernel wise, it looks approximately the same. The major difference being it also needs to keep track when to wait for the reader to give it new tiles for new frequency factors. And keeping in mind that Dst is double buffered. It must always unpack the frequency factor tiles to Dst to ensure data the correct data is avaliable (or alternatively disable double buffering, but that is costly performance wise).

// In rope_tile
for(int i=0;i<2;i++) {
    int ff_idx = 96+((vec_offset/32)%2)*8+i;
    vFloat ff = vFloat(dst_reg[ff_idx]);
    vFloat d0 = ff;
    vFloat d1 = ff;
    vFloat d2 = ff;
    vFloat d3 = ff;
    sfpi::subvec_transp(d0, d1, d2, d3);
    vFloat r = _reciprocal_compat_<4>(d0);
    v_if(ff < 0) {
        r = -r;
    }
    v_endif;
    dst_reg[ff_idx] = r;
}

#ifdef HAS_FREQ_FACTOR
    int ff_idx = 96+((vec_offset/32)%2)*8+i;
    freq = freq * vFloat(dst_reg[ff_idx]);
#endif

// In main kernel loop
for(uint32_t active_id=active_begin; active_id<active_end; active_id++) {

    ...
    #ifdef HAS_FREQ_FACTOR
    uint32_t ff_idx = w/2;
    bool process_ff = last_ff_idx != ff_idx;
    if(last_ff_idx != ff_idx) {
        if(last_ff_idx != uint32_t(-1)) {
            cb_pop_front(cb_in2, 1);
        }
        cb_wait_front(cb_in2, 1);
    }
    last_ff_idx = ff_idx;
    #endif

    ...
    #ifdef HAS_FREQ_FACTOR
    // Must always unpack freq_factor to dst as it is double buffered
    // The data unpacked last round will be unavaliable
    copy_tile_init(cb_in2);
    copy_tile(cb_in2, 0, 3);
    #endif
}

That's gonna be the end of the journey with RoPE. Things I care works. There are other variants of RoPE I haven't support yet. The implementation is not as fast as it can be. But good enough for my need for now. And I can always add support and optimize later.

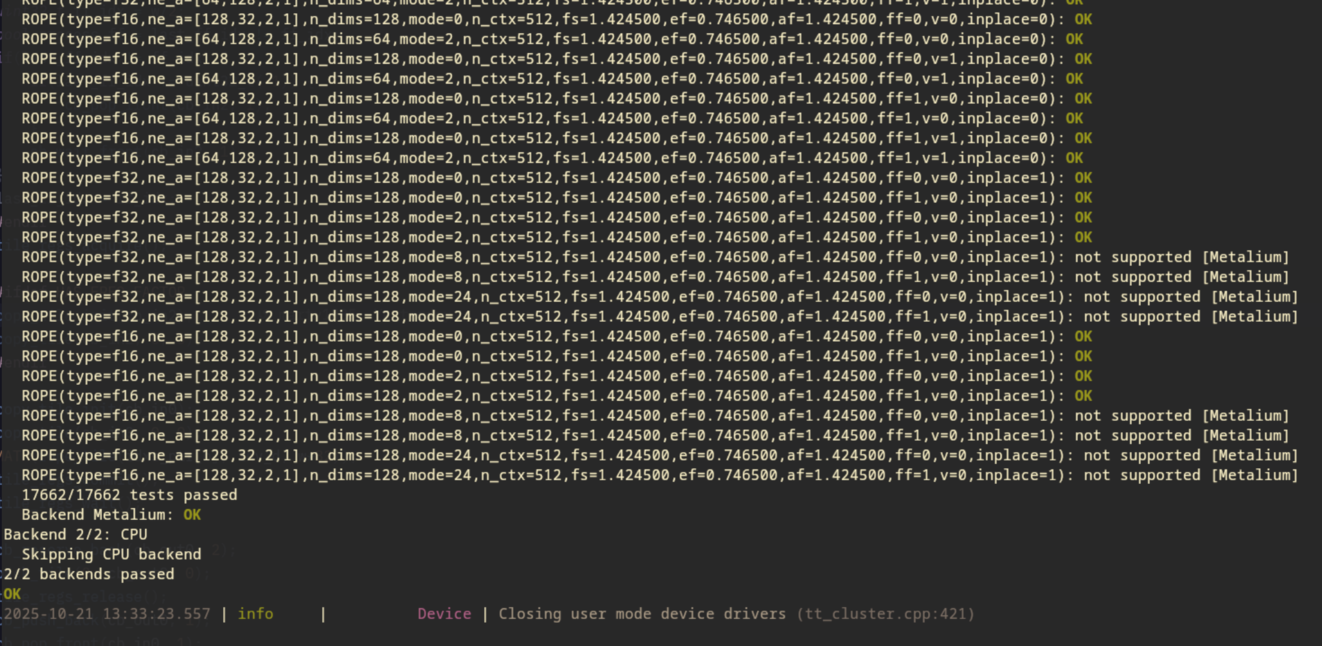
Debugging tips

It makes sense but really takes a while to figure out, Devices created through TTNN (not Metalium) enables the "Persistent Kernel Cache" feature by default. That cache only recognizes the file path and the Metalium commit hash as the cache key. Disable the persistent cache for debugging kernels if you are working with the TTNN layer. Otherwise you will run into weird stale cache and be confused why your code is not getting through.

And you can print values in Dst using dprint_tensix_dest_reg like so. Ofc you'll need to set TT_METAL_DPRINT_CORES to enable debug prints in the runtime:

#include <debug/dpring_tensix.h>

dprint_tensix_dest_reg(/*tile_id*/3);

Yeah that's a VERY long journey getting one operator working on GGML. But hopefully it showcases what it takes, the process and the how to add unsupported operator to TTNN using Metalium. etc. etc.. I have drank my share of beer and coffee to get things going. Hope you learned something.

Special Thanks

Thanks to the following person(s) for help proof read this post

• Fleetwood